
【題目】某商場試銷一種成本為每件60元的服裝,規定試銷期間銷售單價不低于成本單價,且獲利不得高于45%,經試銷發現,銷售量![]() (件)與銷售單價
(件)與銷售單價![]() (元)符合一次函數
(元)符合一次函數![]() ,且
,且![]() 時,
時,![]() ;
;![]() 時,
時,![]() .
.
(1)求一次函數![]() 的表達式;
的表達式;
(2)若該商場獲得利潤為![]() 元,試寫出利潤
元,試寫出利潤![]() 與銷售單價
與銷售單價![]() 之間的關系式;銷售單價定為多少元時,商場可獲得最大利潤,最大利潤是多少元?
之間的關系式;銷售單價定為多少元時,商場可獲得最大利潤,最大利潤是多少元?
(3)若該商場獲得利潤不低于500元,試確定銷售單價![]() 的范圍.
的范圍.
【答案】解:(1)一次函數的表達式為![]()
(2)當銷售單價定為87元時,商場可獲得最大利潤,最大利潤是891元
(3)銷售單價![]() 的范圍是
的范圍是![]() .
.
【解析】
試題(1)列出二元一次方程組解出k與b的值可求出一次函數的表達式.
(2)依題意求出W與x的函數表達式可推出當x=87時商場可獲得最大利潤.
(3)由w=500推出x2﹣180x+7700=0解出x的值即可.
試題解析:(1)根據題意得:![]() ,解得k=﹣1,b=120.所求一次函數的表達式為
,解得k=﹣1,b=120.所求一次函數的表達式為![]() ;
;
(2)![]() =
=![]() ,∵拋物線的開口向下,∴當x<90時,W隨x的增大而增大,而銷售單價不低于成本單價,且獲利不得高于45%,即60≤x≤60×(1+45%),∴60≤x≤87,∴當x=87時,W=
,∵拋物線的開口向下,∴當x<90時,W隨x的增大而增大,而銷售單價不低于成本單價,且獲利不得高于45%,即60≤x≤60×(1+45%),∴60≤x≤87,∴當x=87時,W=![]() =891,∴當銷售單價定為87元時,商場可獲得最大利潤,最大利潤是891元.
=891,∴當銷售單價定為87元時,商場可獲得最大利潤,最大利潤是891元.
(3)令![]() =500,解方程
=500,解方程![]() ,
,![]() 解得
解得![]() ,
,![]() ,又∵60≤
,又∵60≤![]() ≤87 ,所以當
≤87 ,所以當![]() ≥500時,70≤
≥500時,70≤![]() ≤87.
≤87.


科目:初中數學 來源: 題型:
【題目】如圖,在菱形ABCD中,點P是BC邊上一動點,連結AP,AP的垂直平分線交BD于點G,交 AP于點E,在P點由B點到C點的運動過程中,∠APG的大小變化情況是( )

A. 變大 B. 先變大后變小 C. 先變小后變大 D. 不變
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】李明準備進行如下操作實驗,把一根長40 cm的鐵絲剪成兩段,并把每段首尾相連各圍成一個正方形.
(1)要使這兩個正方形的面積之和等于58 cm2,李明應該怎么剪這根鐵絲?
(2)李明認為這兩個正方形的面積之和不可能等于48 cm2,你認為他的說法正確嗎?請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】將圖中的![]() 型(正方形)、
型(正方形)、![]() 型(菱形)、
型(菱形)、![]() 型(等腰直角三角形)紙片分別放在
型(等腰直角三角形)紙片分別放在![]() 個盒子中,盒子的形狀、大小、質地都相同,再將這
個盒子中,盒子的形狀、大小、質地都相同,再將這![]() 個盒子裝入一只不透明的袋子中.
個盒子裝入一只不透明的袋子中.
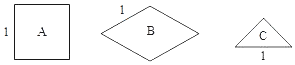
(1)攪勻后從中摸出![]() 個盒子,盒中的紙片既是軸對稱圖形又是中心對稱圖形的概率是 ;
個盒子,盒中的紙片既是軸對稱圖形又是中心對稱圖形的概率是 ;
(2)攪勻后先從中摸出![]() 個盒子(不放回),再從余下的
個盒子(不放回),再從余下的![]() 個盒子中摸出
個盒子中摸出![]() 個盒子,把摸出的
個盒子,把摸出的![]() 個盒中的紙片長度相等的邊拼在一起,求拼成的圖形是軸對稱圖形的概率.(不重疊無縫隙拼接)
個盒中的紙片長度相等的邊拼在一起,求拼成的圖形是軸對稱圖形的概率.(不重疊無縫隙拼接)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】甲乙兩名戰士在相同條件下各射擊10次,每次命中的環數分別是:
甲:8,6,7,8,6,5,9,10,4,7 乙:6,7,7,6,7,8,7,9,8,5
(1)分別求出兩組數據的方差和標準差;
(2)根據計算結果,評價一下兩名戰士的射擊情況.
查看答案和解析>>
科目:初中數學 來源: 題型:
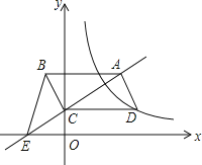
【題目】如圖,平行四邊形ABCD的頂點C在y軸正半軸上,CD平行于x軸,直線AC交x軸于點E,BC⊥AC,連接BE,反比例函數![]() (x>0)的圖象經過點D.已知S△BCE=1,則k=______.
(x>0)的圖象經過點D.已知S△BCE=1,則k=______.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某公司從年初以來累計利潤S(萬元)與時間t(月)之間的關系(即前t個月的利潤總和S和t之間的關系)為二次函數關系.試根據圖象提供的信息,解答下列問題:
(1)求累計利潤S(萬元)與時間t(月)之間的函數表達式;
(2)截至幾月末該公司累計利潤可達16萬元?
(3)第10個月該公司所獲利潤是多少萬元?
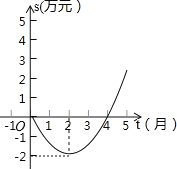
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,直線![]() 與反比例函數
與反比例函數![]() 在第一象限內的圖象相交于點
在第一象限內的圖象相交于點![]() .
.
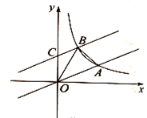
(1)求反比例函數的解析式;
(2)將直線![]() 向上平移后與反比例函數圖象在第一象限內交于點
向上平移后與反比例函數圖象在第一象限內交于點![]() ,與
,與![]() 軸交于點
軸交于點![]() ,且
,且![]() 的面積為
的面積為![]() ,求直線
,求直線![]() 的解析式.
的解析式.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com