先閱讀下列第(1)題的解答過程:
(1)已知a,β是方程x
2+2x-7=0的兩個實數根,求a
2+3β
2+4β的值.
解法1:∵a,β是方程x
2+2x-7=0的兩個實數根,
∴a
2+2a-7=0,β
2+2β-7=0,且a+β=-2.
∴a
2=7-2a,β
2=7-2β.
∴a
2+3β
2+4β=7-2a+3(7-2β)+4β=28-2(a+β)=28-2×(-2)=32.
解法2:由求根公式得a=1+2
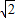
,β=-1-2
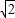
.
∴a
2+3β
2+4β=(-1+2
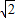
)
2+3(-1-2
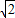
)
2+4(-1-2
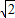
)
=9-4
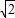
+3(9+4
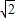
)-4-8
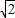
=32.
當a=-1-2
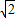
,β=-1+2
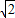
時,同理可得a
2+3β
2+4β=32.
解法3:由已知得a+β=-2,aβ=-7.
∴a
2+β
2=(a+β)
2-2aβ=18.
令a
2+3β
2+4β=A,β
2+3a
2+4a=B.
∴A+B=4(a
2+β
2)+4(a+β)=4×18+4×(-2)=64.①
A-B=2(β
2-a
2)+4(β-a)=2(β+a)(β-a)+4(β-a)=0.②
①+②,得2A=64,∴A=32.
請仿照上面的解法中的一種或自己另外尋注一種方法解答下面的問題:
(2)已知x
1,x
2是方程x
2-x-9=0的兩個實數根,求代數式x
13+7x
22+3x
2-66的值.

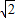 ,β=-1-2
,β=-1-2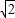 .
.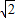 )2+3(-1-2
)2+3(-1-2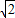 )2+4(-1-2
)2+4(-1-2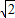 )
)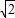 +3(9+4
+3(9+4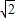 )-4-8
)-4-8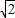 =32.
=32.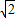 ,β=-1+2
,β=-1+2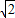 時,同理可得a2+3β2+4β=32.
時,同理可得a2+3β2+4β=32.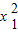 =x1+9,
=x1+9,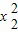 =x2+9,然后將原式變形為x1(x1+9)+7(x2+9)+3x2-66,整理后代入即可求值.
=x2+9,然后將原式變形為x1(x1+9)+7(x2+9)+3x2-66,整理后代入即可求值.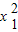 -x1-9=0,
-x1-9=0,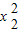 -x2-9=0,
-x2-9=0,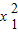 =x1+9,
=x1+9,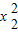 =x2+9.
=x2+9.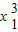 +7
+7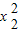 +3x2-66
+3x2-66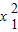 +9x1+10x2-3
+9x1+10x2-3

 名校課堂系列答案
名校課堂系列答案 ,β=-1-2
,β=-1-2 .
. )2+3(-1-2
)2+3(-1-2 )2+4(-1-2
)2+4(-1-2 )
) +3(9+4
+3(9+4 )-4-8
)-4-8 =32.
=32. ,β=-1+2
,β=-1+2 時,同理可得a2+3β2+4β=32.
時,同理可得a2+3β2+4β=32.