
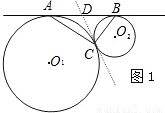
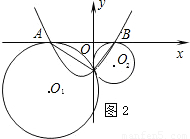
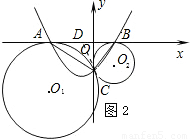
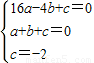 ,
,
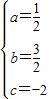 ,
, x2+
x2+ x-2.
x-2. ,0),
,0),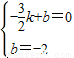 ,
,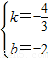 ,
, x-2,
x-2, x-2垂直,
x-2垂直, x-2.
x-2. ,-
,-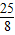 ),
), ×
× -2=-
-2=-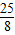 ,故這條拋物線的頂點落在兩圓的連心O1O2上.
,故這條拋物線的頂點落在兩圓的連心O1O2上.

 名校課堂系列答案
名校課堂系列答案科目:初中數學 來源: 題型:
| ||
查看答案和解析>>
科目:初中數學 來源: 題型:
 (2004•呼和浩特)如圖,已知M是?ABCD的AB邊的中點,CM交BD于E,則圖中陰影部分的面積與?ABCD的面積之比是( )
(2004•呼和浩特)如圖,已知M是?ABCD的AB邊的中點,CM交BD于E,則圖中陰影部分的面積與?ABCD的面積之比是( )
|
|
|
|
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com