
 如圖,已知△ABC中,AB=BC,∠ABC=90°,把一塊含30°角的直角三角板DEF的直角頂點D放在AC的中點上(直角三角板的短直角邊為DE,長直角邊為DF),將直角三角板DEF繞D點按逆時針方向旋轉(zhuǎn)至如圖的位置,延長AB交DE于M,延長BC交DF于N,
如圖,已知△ABC中,AB=BC,∠ABC=90°,把一塊含30°角的直角三角板DEF的直角頂點D放在AC的中點上(直角三角板的短直角邊為DE,長直角邊為DF),將直角三角板DEF繞D點按逆時針方向旋轉(zhuǎn)至如圖的位置,延長AB交DE于M,延長BC交DF于N,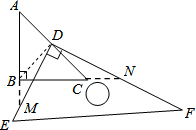
 ∠ABC=45°,
∠ABC=45°,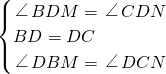 ,
, ∠ABC=45°,求出∠DBM=135°=∠DCN,∠BDM=∠CDN,根據(jù)ASA推出△CDN≌△BDM即可.
∠ABC=45°,求出∠DBM=135°=∠DCN,∠BDM=∠CDN,根據(jù)ASA推出△CDN≌△BDM即可.

 一卷搞定系列答案
一卷搞定系列答案 名校作業(yè)本系列答案
名校作業(yè)本系列答案 輕巧奪冠周測月考直通名校系列答案
輕巧奪冠周測月考直通名校系列答案科目:初中數(shù)學(xué) 來源: 題型:
 如圖,已知△ABC中,BC=8,BC邊上的高h=4,D為BC上一點,EF∥BC交AB于E,交AC于F(EF不過A、B),設(shè)E到BC的距離為x,△DEF的面積為y,那么y關(guān)于x的函數(shù)圖象大致是( )
如圖,已知△ABC中,BC=8,BC邊上的高h=4,D為BC上一點,EF∥BC交AB于E,交AC于F(EF不過A、B),設(shè)E到BC的距離為x,△DEF的面積為y,那么y關(guān)于x的函數(shù)圖象大致是( )查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com