
【題目】如圖,已知在△ABC中,∠B=90°,AB=8cm,BC=6cm,點P從點A開始沿△ABC的邊做逆時針運動,且速度為每秒1cm;點Q從點B開始沿△ABC的邊做逆時針運動,且速度為每秒2cm,他們同時出發,設運動時間為t秒.
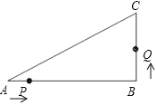
(1)出發2秒后,P,Q兩點間的距離為多少cm?
(2)在運動過程中,△PQB能形成等腰三角形嗎?若能,請求出幾秒后第一次形成等腰三角形;若不能,則說明理由.
(3)出發幾秒后,線段PQ第一次把△ABC的周長分成相等兩部分?
【答案】(1)![]() cm;(2)在運動過程中,△PQB能形成等腰三角形,出發后
cm;(2)在運動過程中,△PQB能形成等腰三角形,出發后![]() 秒后第一次形成等腰三角形.(3)4.
秒后第一次形成等腰三角形.(3)4.
【解析】
試題分析:(1)求出AP、BP、BQ,根據勾股定理求出PQ即可.
(2)根據等腰直角三角形得出BP=BQ,代入得出方程,求出方程的解即可.
(3)根據周長相等得出10+t+(6-2t)=8-t+2t,求出即可.
試題解析:
(1)∵出發2秒后AP=2cm,
∴BP=8-2=6(cm),
BQ=2×2=4(cm),
在Rt△PQB中,由勾股定理得:![]() (cm)
(cm)
即出發2秒后,求PQ的長為![]() cm
cm
(2)在運動過程中,△PQB能形成等腰三角形,
AP=t,BP=AB-AP=8-t;BQ=2t
由PB=BQ得:8-t=2t
解得t=![]() (秒),
(秒),
即出發后![]() 秒后第一次形成等腰三角形.
秒后第一次形成等腰三角形.
(3)Rt△ABC中由勾股定理得:![]() (cm);
(cm);
∵AP=t,BP=AB-AP=8-t,BQ=2t,QC=6-2t,
又∵線段PQ第一次把直角三角形周長分成相等的兩部分,
∴由周長相等得:AC+AP+QC=PB+BQ
10+t+(6-2t)=8-t+2t
解得t=4(cm)
即從出發4秒后,線段PQ第一次把直角三角形周長分成相等的兩部分.


 沖刺100分1號卷系列答案
沖刺100分1號卷系列答案 期末好成績系列答案
期末好成績系列答案科目:初中數學 來源: 題型:
【題目】如圖,在ABCD中,點O是邊BC的中點,連接DO并延長,交AB延長線于點E,連接BD,EC.
(1)求證:四邊形BECD是平行四邊形;
(2)若∠A=50°,則當∠BOD= ______ °時,四邊形BECD是矩形.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖![]() ,平行四邊形
,平行四邊形![]() 中,對角線
中,對角線![]() 、
、![]() 交于點
交于點![]() .將直線
.將直線![]() 繞點
繞點![]() 順時針旋轉分別交
順時針旋轉分別交![]() 、
、![]() 于點
于點![]() 、
、![]() .
.

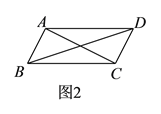
(![]() )在旋轉過程中,線段
)在旋轉過程中,線段![]() 與
與![]() 的數量關系是__________.
的數量關系是__________.
(![]() )如圖
)如圖![]() ,若
,若![]() ,當旋轉角至少為__________
,當旋轉角至少為__________![]() 時,四邊形
時,四邊形![]() 是平行四邊形,并證明此時的四邊形是
是平行四邊形,并證明此時的四邊形是![]() 是平行四邊形.
是平行四邊形.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】數學課上, 老師要求同學們利用三角板畫兩條平行線.老師說苗苗和小華兩位同學畫法都是正確的,兩位同學的畫法如下:
苗苗的畫法:

①將含30°角的三角尺的最長邊與直線a重合,另一塊三角尺最長邊與含30°角的三角尺的最短邊緊貼;
②將含30°角的三角尺沿貼合邊平移一段距離,畫出最長邊所在直線b,則b//a.
小華的畫法:

①將含30°角三角尺的最長邊與直線a重合,用虛線做出一條最短邊所在直線;
②再次將含30°角三角尺的最短邊與虛線重合,畫出最長邊所在直線b,則b//a.
請在苗苗和小華兩位同學畫平行線的方法中選出你喜歡的一種,并寫出這種畫圖的依據.
答:我喜歡__________同學的畫法,畫圖的依據是__________.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,拋物線y=﹣x2+2x+m+1交x軸于點A(a,0)和B(b,0),交y軸于點C,拋物線的頂點為D,下列三個判斷中:
①當x>0時,y>0;
②若a=﹣1,則b=4;
③拋物線上有兩點P(x1 , y1)和Q(x2 , y2),若x1<1<x2 , 且x1+x2>2,則y1>y2;正確的是( )
A.①
B.②
C.③
D.①②③都不對
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知點O是直線AB上的一點,∠COE=90°,OF是∠AOE的平分線.
(1)當點C,E,F在直線AB的同側時(如圖①所示),試說明∠BOE=2∠COF.
(2)當點C與點E,F在直線AB的兩側時(如圖②所示),(1)中的結論是否仍然成立?請給出你的結論,并說明理由.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下列變形中:
①由方程![]() =2去分母,得x﹣12=10;
=2去分母,得x﹣12=10;
②由方程![]() x=
x=![]() 兩邊同除以
兩邊同除以![]() ,得x=1;
,得x=1;
③由方程6x﹣4=x+4移項,得7x=0;
④由方程2﹣![]() 兩邊同乘以6,得12﹣x﹣5=3(x+3).
兩邊同乘以6,得12﹣x﹣5=3(x+3).
錯誤變形的個數是( )個.
A. 4 B. 3 C. 2 D. 1
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某校七年級(1)班體育委員統計了全班同學60秒跳繩次數,并列出了下面的不完整頻數分布表和不完整的頻數分布直方圖.根據圖表中的信息解答問題
組別 | 跳繩次數 | 頻數 |
A | 60≤x<80 | 2 |
B | 80≤x<100 | 6 |
C | 100≤x<120 | 18 |
D | 120≤x<140 | 12 |
E | 140≤x<160 | a |
F | 160≤x<180 | 3 |
G | 180≤x<200 | 1 |
合計 | 50 | |
(1)求a的值;
(2)求跳繩次數x在120≤x<180范圍內的學生的人數;
(3)補全頻數分布直方圖,并指出組距與組數分別是多少?

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com