

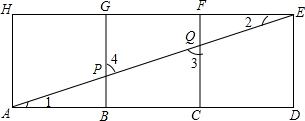
 (1)∵正方形ABGH、BCFG、CDEF是全等正方形,
(1)∵正方形ABGH、BCFG、CDEF是全等正方形, =
= ,
, •DE=
•DE=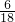 ×6=2(cm)
×6=2(cm) 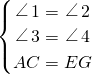
 =
= ,所以根據正方形的性質將相關線段的長度代入并求值即可;
,所以根據正方形的性質將相關線段的長度代入并求值即可;

科目:初中數學 來源: 題型:

查看答案和解析>>
科目:初中數學 來源:2013年安徽省安慶市中考數學一模試卷(解析版) 題型:解答題
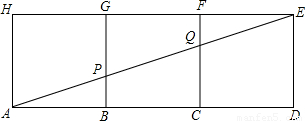
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com