
操作與探索:
已知點O為直線AB上一點,作射線OC,將直角三角板ODE放置在直線上方(如圖①),使直角頂點與點O重合,一條直角邊OD重疊在射線OA上,將三角板繞點O旋轉
(1)當三角板旋轉到如圖②的位置時,若OD平分∠AOC,試說明OE也平分∠BOC.
(2)若OC⊥AB,垂足為點O(如圖③),請直接寫出與∠DOB互補的角
(3)若∠AOC=135°(如圖④),三角板繞點O按順時針從如圖①的位置開始旋轉,到OE邊與射線OB重合結束. 請通過操作,探索:在旋轉過程中,∠DOB ∠COE的差是否發生變化?若不變,請求出這個差值;若變化,請用含有n(n為三角板旋轉的度數)的代數式表示這個差.
∠COE的差是否發生變化?若不變,請求出這個差值;若變化,請用含有n(n為三角板旋轉的度數)的代數式表示這個差.
(1)由OD平分∠AOC可得∠AOD=∠COD,由∠DOE=90°可得∠AOD+∠EOB=90°,∠COD+∠COE=90°,即可證得結論;(2)∠AOD、∠COE;
(3)①若n≤45°,∠DOB ∠COE=135°,②若n>45°,∠DOB
∠COE=135°,②若n>45°,∠DOB ∠COE=225°
∠COE=225° 2n
2n
解析試題分析:(1)由OD平分∠AOC可得∠AOD=∠COD,由∠DOE=90°可得∠AOD+∠EOB=90°,∠COD+∠COE=90°,即可證得結論;
(2)由OC⊥AB可得∠AOD+∠COD=90°,由∠DOE=90°可得∠COD+∠COE=90°,即可得到∠AOD=∠COE,從而可以求得與∠DOB互補的角;
(3)由于旋轉45°時,OE與OC重合,故要分n≤45°與n>45°兩種情況分析.
(1)∵OD平分∠AOC
∴∠AOD=∠COD
∵∠DOE=90°
∴∠AOD+∠EOB=90°,∠COD+∠COE=90°
∴∠COE=∠EOB
∴OE也平分∠BOC;
(2)∵OC⊥AB,∠DOE=90°
∴∠AOD+∠COD=90°,∠COD+∠COE=90°
∴∠AOD=∠COE
∴與∠DOB互補的角為∠AOD、∠COE;
(3)①若n≤45°,∠DOB ∠COE=(180°-n)-(45°-n)=180°-n-45°+n=135°,
∠COE=(180°-n)-(45°-n)=180°-n-45°+n=135°,
②若n>45°,∠DOB ∠COE=(180°-n)-(n-45°)=180°-n-n+45°=225°
∠COE=(180°-n)-(n-45°)=180°-n-n+45°=225° 2n.
2n.
考點:旋轉的性質,角平分線的性質,互補的定義,同角的余角相等
點評:解答本題的關鍵是注意直角三角板的問題往往應用到同角的余角相等的知識,同時熟記旋轉對應邊是夾角是旋轉角.


 名校課堂系列答案
名校課堂系列答案科目:初中數學 來源: 題型:
查看答案和解析>>
科目:初中數學 來源:2012屆江蘇省淮安市清浦區清浦中學中考模擬試卷2數學試卷(帶解析) 題型:解答題
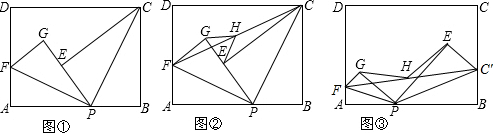
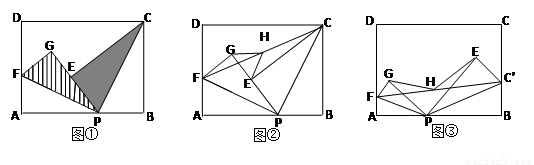
已知點P是矩形ABCD邊AB上的任意一點(與點A、B不重合)
(1)如圖①,現將△PBC沿PC翻折得到△PEC;再在AD上取一點F,將△PAF沿PF翻折得到△PGF,并使得射線PE、PG重合,試問FG與CE的位置關系如何,請說明理由;
(2)在(1)中,如圖②,連接FC,取FC的中點H,連接GH、EH,請你探索線段GH和線段EH的大小關系,并說明你的理由;
(3)如圖③,分別在AD、BC上取點F、C’,使得∠APF=∠BPC’,與(1)中的操作相類似,即將△PAF沿PF翻折得到△PFG,并將△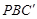 沿
沿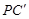 翻折得到△
翻折得到△ ,連接
,連接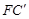 ,取
,取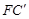 的中點H,連接GH、EH,試問(2)中的結論還成立嗎?請說明理由.
的中點H,連接GH、EH,試問(2)中的結論還成立嗎?請說明理由.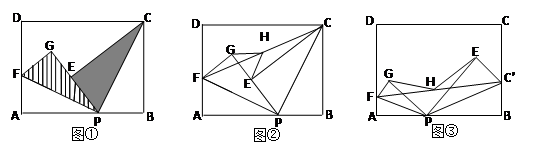
查看答案和解析>>
科目:初中數學 來源:2012-2013學年江蘇泰興實驗初級中學七年級上期末考試數學試卷(解析版) 題型:解答題
操作與探索:
已知點O為直線AB上一點,作射線OC,將直角三角板ODE放置在直線上方(如圖①),使直角頂點與點O重合,一條直角邊OD重疊在射線OA上,將三角板繞點O旋轉

(1)當三角板旋轉到如圖②的位置時,若OD平分∠AOC,試說明OE也平分∠BOC.
(2)若OC⊥AB,垂足為點O(如圖③),請直接寫出與∠DOB互補的角
(3)若∠AOC=135°(如圖④),三角板繞點O按順時針從如圖①的位置開始旋轉,到OE邊與射線OB重合結束. 請通過操作,探索:在旋轉過程中,∠DOB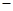 ∠COE的差是否發生變化?若不變,請求出這個差值;若變化,請用含有n(n為三角板旋轉的度數)的代數式表示這個差.
∠COE的差是否發生變化?若不變,請求出這個差值;若變化,請用含有n(n為三角板旋轉的度數)的代數式表示這個差.
查看答案和解析>>
科目:初中數學 來源:2011-2012學年江蘇省淮安市中考模擬試卷2數學試卷(解析版) 題型:解答題
已知點P是矩形ABCD邊AB上的任意一點(與點A、B不重合)
(1)如圖①,現將△PBC沿PC翻折得到△PEC;再在AD上取一點F,將△PAF沿PF翻折得到△PGF,并使得射線PE、PG重合,試問FG與CE的位置關系如何,請說明理由;
(2)在(1)中,如圖②,連接FC,取FC的中點H,連接GH、EH,請你探索線段GH和線段EH的大小關系,并說明你的理由;
(3)如圖③,分別在AD、BC上取點F、C’,使得∠APF=∠BPC’,與(1)中的操作相類似,即將△PAF沿PF翻折得到△PFG,并將△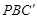 沿
沿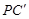 翻折得到△
翻折得到△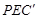 ,連接
,連接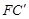 ,取
,取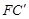 的中點H,連接GH、EH,試問(2)中的結論還成立嗎?請說明理由.
的中點H,連接GH、EH,試問(2)中的結論還成立嗎?請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com