
【題目】如圖,點O在直線AB上,OE、OD分別是∠AOC、∠BOC的平分線.
(1)∠AOE的補角是∠____;∠BOD的余角是______;
(2)若∠AOC=118°,求∠COD的度數;
(3)射線OD與OE之間有什么特殊的位置關系?為什么?
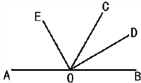
【答案】(1)BOE,∠AOE和∠COE;(2)31°;(3)OD⊥OE
【解析】試題分析:
(1)根據圖形結合“補角的定義”可得∠AOE的補角是∠BOE;由OE、OD分別是∠AOC、∠BOC的平分線,可得∠COE=∠AOE=![]() ∠AOC,∠COD=∠BOD=
∠AOC,∠COD=∠BOD=![]() ∠BOC,從而可證得∠COE+∠COD=∠DOE=90°,由此可得∠BOD+∠COE=90°,∠BOD+∠AOE=90°,從而可知,∠BOD的余角是∠AOE和∠COE;
∠BOC,從而可證得∠COE+∠COD=∠DOE=90°,由此可得∠BOD+∠COE=90°,∠BOD+∠AOE=90°,從而可知,∠BOD的余角是∠AOE和∠COE;
(2)由∠AOC的度數可先求得∠BOC的度數,再由OD平分∠BOC即可得到∠COD的度數;
(3)由(1)可知∠DOE=90°,由此就可得到OE⊥OD.
試題解析:
(1)∵點O在直線AB上,
∴∠AOE+∠BOE=180°,∠AOC+∠BOC=180°,
∴∠AOE的補角是∠BOE.
∵OE、OD分別是∠AOC、∠BOC的平分線,
∴∠COE=∠AOE=![]() ∠AOC,∠COD=∠BOD=
∠AOC,∠COD=∠BOD=![]() ∠BOC,
∠BOC,
∴∠COE+∠COD=![]() (∠AOC+∠BOC)=
(∠AOC+∠BOC)= ![]() ∠AOB=90°,
∠AOB=90°,
∴∠BOD+∠COE=90°,∠BOD+∠AOE=90°,
∴在圖中,∠BOD的余角是∠AOE和∠COE;
(2)由(1)可知,∠AOC+∠BOC=180°,∠COD=∠BOD=![]() ∠BOC,
∠BOC,
∴∠BOC=180°-∠AOC=180°-118°=62°,
∴∠COD=62°×![]() =31°;
=31°;
(3)射線OD與OE之間的位置關系是:OD⊥OE,理由如下:
由(1)可知:∠DOE=∠COE+∠COD=![]() (∠AOC+∠BOC)=
(∠AOC+∠BOC)= ![]() ∠AOB=90°,
∠AOB=90°,
∴OD⊥OE.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:初中數學 來源: 題型:
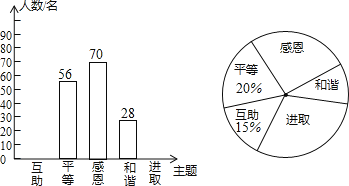
【題目】某校開展了“互助、平等、感恩、和諧、進取”主題班會活動,活動后,就活動的5個主題進行了抽樣調查(每位同學只選取最關注的一個),根據調查結果繪制了兩幅不完整的統計圖,根據圖中提供的信息,解答下列問題:
(1)這次調查的學生共有多少名?
(2)請將條形統計圖補充完整;并寫出這次主題班會調查結果的眾數是 ;中位數落在的區域是 .
(3)若該校學生人數為800人,請根據上述調查結果,估計該校學生中“感恩”的人數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】甲、乙兩家超市以相同的價格出售同樣的商品,為了吸引顧客,各自推出不同的優惠方案:在甲超市累計購買商品超出300元之后,超出部分按原價8折優惠;在乙超市累計購買商品超出200元之后,超出部分按原價8.5折優惠.設顧客預計累計購物![]() 元(
元(![]() ).
).
(1)請用含![]() 的代數式分別表示顧客在兩家超市購物所付的費用;
的代數式分別表示顧客在兩家超市購物所付的費用;
(2)李明準備購買500元的商品,你認為他應該去哪家超市?請說明理由;
(3)計算一下,李明購買多少元的商品時,到兩家超市購物所付的費用一樣?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】計算:(1)(+ 3.4)+(-5![]() )-(-4
)-(-4![]() )-(+2
)-(+2![]() );(2)-4+(-3
);(2)-4+(-3![]() )×
)×![]() -(- 24)÷4;
-(- 24)÷4;
(3)(-1![]() +2
+2![]() -1
-1![]() )÷(-
)÷(-![]() );(4)-12018-(1-0.5)×
);(4)-12018-(1-0.5)×![]() ×[2-(-3)3].
×[2-(-3)3].
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】【探索新知】
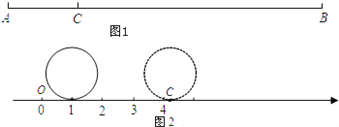
如圖1,點C將線段AB分成AC和BC兩部分,若BC= ![]() AC,則稱點C是線段AB的圓周率點,線段AC、BC稱作互為圓周率伴侶線段.
AC,則稱點C是線段AB的圓周率點,線段AC、BC稱作互為圓周率伴侶線段.
(1)若AC=3,則AB=_____;
(2)若點D也是圖1中線段AB的圓周率點(不同于C點),則AC_____DB;(填“=”或“≠”)
【深入研究】
如圖2,現有一個直徑為1個單位長度的圓片,將圓片上的某點與數軸上表示1的點重合,并把圓片沿數軸向右無滑動地滾動1周,該點到達點C的位置.
(3)若點M、N均為線段OC的圓周率點,求線段MN的長度.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在矩形ABCD中,點E,F分別在邊AB,BC上,且AE= ![]() AB,將矩形沿直線EF折疊,點B恰好落在AD邊上的點P處,連接BP交EF于點Q,對于下列結論:①EF=2BE;②PF=2PE;③FQ=4EQ;④△PBF是等邊三角形.其中正確的是( )
AB,將矩形沿直線EF折疊,點B恰好落在AD邊上的點P處,連接BP交EF于點Q,對于下列結論:①EF=2BE;②PF=2PE;③FQ=4EQ;④△PBF是等邊三角形.其中正確的是( ) 
A.①②
B.②③
C.①③
D.①④
查看答案和解析>>
科目:初中數學 來源: 題型:
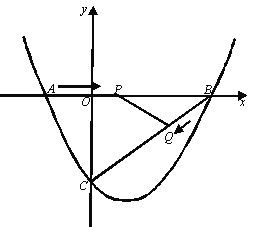
【題目】如圖,在平面直角坐標系中,拋物線![]() 與x軸交于點A(
與x軸交于點A(![]() ,0)、B(4,0)兩點,與y軸交于點C。
,0)、B(4,0)兩點,與y軸交于點C。
(1)求拋物線的解析式;
(2)點P從A點出發,在線段AB上以每秒3個單位長度的速度向B點運動,同時點Q從B點出發,在線段BC上以每秒1個單位長度向C點運動。其中一個點到達終點時,另一個點也停止運動。當△PBQ存在時,求運動多少秒使△PBQ的面積最大,最多面積是多少?
(3)當△PBQ的面積最大時,在BC下方的拋物線上存在點K,使S△CBK∶S△PBO=5∶2,求K點坐標。
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com