解方程:
(1)x2+8x+16=0
(2)4x2+19x-5=0
(3)(x-5)2=2(x-5)
(4)(x2-2)2-(x2-2)-6=0.
【答案】
分析:(1)直接用因式分解法解就可以.
(2)可以直接用因式分解法解答;
(3)先移項,然后用因式分解法求解;
(4)先設x
2-2=A,原方程變形為A
2-A-6=0,再用因式分解法求出A的值就可以了.
解答:解:(1)(x+4)
2=0,
∴x+4=0,
∴x
1=x
2=-4;
(2)(4x-1)(x+5)=0;
∴4x-1=0,x+5=0;
∴x
1=

,x
2=-5;
(3)移項,得
(x-5)
2-2(x-5)=0,
(x-5)(x-5-2)=0,
∴x-5=0,x-7=0
∴x
1=5,x
2=7;
(4)x
2-2=A,原方程變形為A
2-A-6=0,
(A-3)(A+2)=0,
∴A
1=3,A
2=-2
當A
1=-2時,
x
2-2=-2,
解得x
1=x
2=0,
當A
2=3時,
x
2-2=3
解得x
3=

,x
4=-
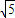
.
故x
1=x
2=0,x
3=
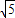
,x
4=-

.
點評:本題考查了換元法解一元二次方程的運用,因式分解法解一元二次方程的運用,在解答中注意計算的正確性,特別是換元法特別容易漏根.

 ,x2=-5;
,x2=-5; ,x4=-
,x4=-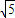 .
.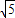 ,x4=-
,x4=- .
.
