
【題目】操作:“如圖1,P是平面直角坐標系中一點(x軸上的點除外),過點P作PC⊥x軸于點C,點C繞點P逆時針旋轉60°得到點Q.”我們將此由點P得到點Q的操作稱為點的T變換.
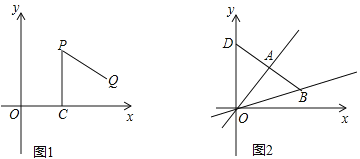
(1)點P(a,b)經過T變換后得到的點Q的坐標為 ;若點M經過T變換后得到點N(6,﹣![]() ),則點M的坐標為 .
),則點M的坐標為 .
(2)A是函數y=![]() x圖象上異于原點O的任意一點,經過T變換后得到點B.
x圖象上異于原點O的任意一點,經過T變換后得到點B.
①求經過點O,點B的直線的函數表達式;
②如圖2,直線AB交y軸于點D,求△OAB的面積與△OAD的面積之比.
【答案】(1)Q(a+![]() b,
b,![]() b);M(9,﹣2
b);M(9,﹣2![]() );(2)①y=
);(2)①y=![]() x;②
x;②![]()
【解析】
試題分析:(1)連接CQ可知△PCQ為等邊三角形,過Q作QD⊥PC,利用等邊三角形的性質可求得CD和QD的長,則可求得Q點坐標;設出M點的坐標,利用P、Q坐標之間的關系可得到點M的方程,可求得M點的坐標;
(2)①可取A(2,![]() ),利用T變換可求得B點坐標,利用待定系數示可求得直線OB的函數表達式;②由待定系數示可求得直線AB的解析式,可求得D點坐標,則可求得AB、AD的長,可求得△OAB的面積與△OAD的面積之比.
),利用T變換可求得B點坐標,利用待定系數示可求得直線OB的函數表達式;②由待定系數示可求得直線AB的解析式,可求得D點坐標,則可求得AB、AD的長,可求得△OAB的面積與△OAD的面積之比.
試題解析:(1)如圖1,連接CQ,過Q作QD⊥PC于點D,
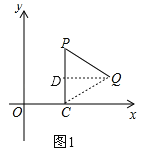
由旋轉的性質可得PC=PQ,且∠CPQ=60°,
∴△PCQ為等邊三角形,
∵P(a,b),
∴OC=a,PC=b,
∴CD=![]() PC=
PC=![]() b,DQ=
b,DQ=![]() PQ=
PQ=![]() b,
b,
∴Q(a+![]() b,
b,![]() b);
b);
設M(x,y),則N點坐標為(x+![]() y,
y,![]() y),
y),
∵N(6,﹣![]() ),
),
∴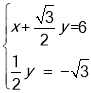 ,解得
,解得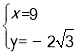 ,
,
∴M(9,﹣2![]() );
);
(2)①∵A是函數y=![]() x圖象上異于原點O的任意一點,
x圖象上異于原點O的任意一點,
∴可取A(2,![]() ),
),
∴2+![]() ×
×![]() =
=![]() ,
,![]() ×
×![]() =
=![]() ,
,
∴B(![]() ,
,![]() ),
),
設直線OB的函數表達式為y=kx,則![]() k=
k=![]() ,解得k=
,解得k=![]() ,
,
∴直線OB的函數表達式為y=![]() x;
x;
②設直線AB解析式為y=k′x+b,
把A、B坐標代入可得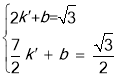 ,解得
,解得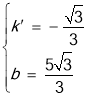 ,
,
∴直線AB解析式為y=﹣![]() x+
x+![]() ,
,
∴D(0,![]() ),且A(2,
),且A(2,![]() ),B(
),B(![]() ,
,![]() ),
),
∴AB=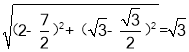 ,AD=
,AD=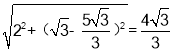 ,
,
∴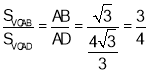 .
.


 明天教育課時特訓系列答案
明天教育課時特訓系列答案 浙江新課程三維目標測評課時特訓系列答案
浙江新課程三維目標測評課時特訓系列答案 周周清檢測系列答案
周周清檢測系列答案 輕巧奪冠周測月考直通高考系列答案
輕巧奪冠周測月考直通高考系列答案科目:初中數學 來源: 題型:
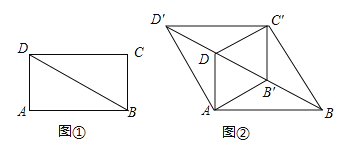
【題目】如圖①,BD是矩形ABCD的對角線,∠ABD=30°,AD=1.將△BCD沿射線BD方向平移到△B'C'D'的位置,使B'為BD中點,連接AB',C'D,AD',BC',如圖②.
(1)求證:四邊形AB'C'D是菱形;
(2)四邊形ABC'D′的周長為 ;
(3)將四邊形ABC'D'沿它的兩條對角線剪開,用得到的四個三角形拼成與其面積相等的矩形,直接寫出所有可能拼成的矩形周長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,AB=AC,AD⊥BC于點D,將△ADC繞點A順時針旋轉,使AC與AB重合,點D落在點E處,AE的延長線交CB的延長線于點M,EB的延長線交AD的延長線于點N.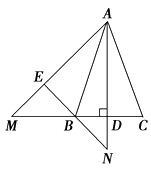
求證:AM=AN.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖所示,飛機在一定高度上沿水平直線飛行,先在點![]() 處測得正前方小島
處測得正前方小島![]() 的俯角為
的俯角為![]() ,面向小島方向繼續飛行
,面向小島方向繼續飛行![]()
![]() 到達
到達![]() 處,發現小島在其正后方,此時測得小島的俯角為
處,發現小島在其正后方,此時測得小島的俯角為![]() .如果小島高度忽略不計,求飛機飛行的高度(結果保留根號).
.如果小島高度忽略不計,求飛機飛行的高度(結果保留根號).

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com