Question

如圖18-1-22，△ABC中，AB=15 cm，AC=24 cm，∠A=60°，求BC的長.

　　 圖18-1-22

Answer 1

答案：
解析：

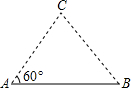
思路分析：因為∠A是一個特殊角，可考慮過點B作BD⊥AC，垂足為D，則∠ABD=30°，所以AD可求.在Rt△BCD中，由勾股定理可求出BC的長. 解：過點B作BD⊥AC，垂足為D. ∵∠A=60°， ∴∠ABD=30°. ∴AD=AB=×15=7.5. BD2=AB2-AD2=152-7.52=168.75. 在Rt△BCD中，由勾股定理得， BC 2=BD2+CD2=168.75+16.52=441. ∴BC=21. 抓住特殊角，構造直角三角形是解決本題的關鍵.本題也可以這樣作輔助線：過點C作CE⊥AB，垂足為E，但過點A作AF⊥BC，垂足為F，則是行不通的.請你想一想為什么？從中可以得到什么啟發？