
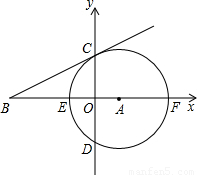
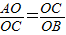 ,求得OB的長,即可得出確定B點坐標,進而可根據B、C坐標用待定系數法求得BC直線的解析式.
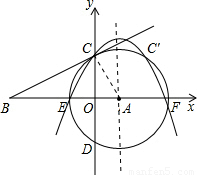
,求得OB的長,即可得出確定B點坐標,進而可根據B、C坐標用待定系數法求得BC直線的解析式. ∠OAC=30°,由于E、F同在拋物線上,因此連接CE后,三角形CEF就與三角形OAC相似.那么C、E、F就是符合條件的點.而根據拋物線的對稱性可知,C點關于拋物線對稱軸的對稱點和E、F組成的直角三角形也應該符合條件.
∠OAC=30°,由于E、F同在拋物線上,因此連接CE后,三角形CEF就與三角形OAC相似.那么C、E、F就是符合條件的點.而根據拋物線的對稱性可知,C點關于拋物線對稱軸的對稱點和E、F組成的直角三角形也應該符合條件.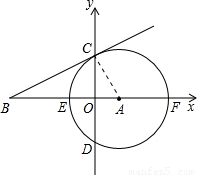 解:(1)方法一:
解:(1)方法一: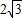 .
.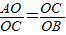 .
.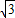 ),點B坐標為(-6,0).
),點B坐標為(-6,0).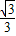 x+2
x+2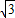 .
.

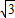 ).
).
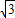 ,
,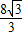 ,
,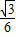 .
.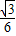 (x-2)2+
(x-2)2+
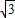 ,
,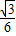 x2+
x2+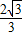 x+2
x+2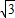 .
. ),如圖.
),如圖.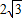 ).
).

 名校課堂系列答案
名校課堂系列答案科目:初中數學 來源: 題型:

查看答案和解析>>
科目:初中數學 來源: 題型:
查看答案和解析>>
科目:初中數學 來源:2007年全國中考數學試題匯編《二次函數》(09)(解析版) 題型:解答題

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com