Question

⊙O的半徑為10，弦AB的長度為12，則在⊙O上到弦AB的距離為1的點有    個，在⊙O上且到弦AB的距離為2的點有    個．

Answer 1

【答案】分析：根據垂徑定理、勾股定理求得在⊙O上到弦AB的最大距離；然后根據圓的對稱性填空．
解答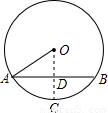：解：根據題意，知AB=12，OA=10．
過圓心O作OC⊥AB交AB于點D．則AD=DB=AB（垂徑定理）；
在直角三角形ADO中，OD=8（勾股定理），
∴CD=2；
∴在⊙O上到弦AB的距離最大是2；
根據圓的對稱性，在⊙O上到弦AB的距離為1的點有4個；在⊙O上到弦AB的距離為2的點有2個．
故答案是：4，2．
點評：本題綜合考查了垂徑定理、勾股定理．解答該題時需要注意：圓的對稱性．