
 ∠OAB=2。
∠OAB=2。
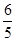 ,-
,-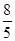 ),使ΔAPC與ΔAOB相似。
),使ΔAPC與ΔAOB相似。 ∠OAB=
∠OAB=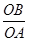
 ∠OAB=2
∠OAB=2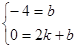 ∴
∴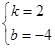

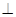 AB交AB于P2,過P2作P1D
AB交AB于P2,過P2作P1D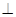 AC于D
AC于D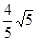
 ∴OD=
∴OD=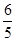 ,
,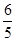 時,y=-
時,y=-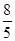
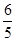 ,-
,-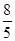 )
)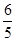 ,-
,-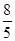 ),使ΔAPC與ΔAOB相似
),使ΔAPC與ΔAOB相似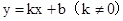 。求直線解析式時需要具備2個已知點坐標,為解題關鍵。題(3)中求證點P是否存在使兩三角形相似。通過證相似三角形的判定定理我們可知必然需要得到兩三角形對應角相等或者對應邊比值相等的條件才能證相似。那么假設存在該點P使形成的三角形與已知的直角三角形相似,通過做輔助垂線,構成兩組對應角相等是解題關鍵,然后得到兩個P點,并通過點P在直線AB上,用直線AB解析式求出點P坐標。
。求直線解析式時需要具備2個已知點坐標,為解題關鍵。題(3)中求證點P是否存在使兩三角形相似。通過證相似三角形的判定定理我們可知必然需要得到兩三角形對應角相等或者對應邊比值相等的條件才能證相似。那么假設存在該點P使形成的三角形與已知的直角三角形相似,通過做輔助垂線,構成兩組對應角相等是解題關鍵,然后得到兩個P點,并通過點P在直線AB上,用直線AB解析式求出點P坐標。

科目:初中數學 來源:不詳 題型:解答題

查看答案和解析>>
科目:初中數學 來源:不詳 題型:解答題
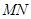 :
: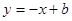 與
與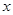 軸交于點
軸交于點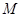 (4,0),與
(4,0),與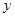 軸交于點
軸交于點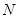 ,長方形
,長方形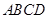 的邊
的邊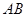 在
在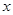 軸上,
軸上,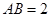 ,
,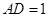 .長方形
.長方形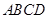 由點
由點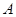 與點
與點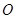 重合的位置開始,以每秒1個單位長度的速度沿
重合的位置開始,以每秒1個單位長度的速度沿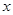 軸正方向作勻速直線運動,當點
軸正方向作勻速直線運動,當點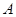 與點
與點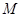 重合時停止運動.設長方形運動的時間為
重合時停止運動.設長方形運動的時間為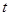 秒,長方形
秒,長方形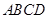 與△
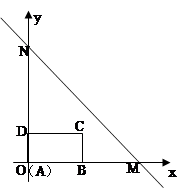
與△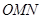 重合部分的面積為
重合部分的面積為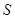 .
.
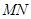 的解析式;
的解析式;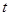 =1時,請判斷點
=1時,請判斷點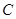 是否在直線
是否在直線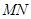 上,并說明理由;
上,并說明理由; 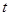 為何值時,點
為何值時,點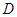 在直線
在直線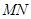 上;
上;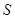 與
與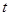 的函數關系式.
的函數關系式.查看答案和解析>>
科目:初中數學 來源:不詳 題型:計算題
 種布料
種布料 ,
, 種布料
種布料 ,現(xiàn)計劃用這兩種布料生產
,現(xiàn)計劃用這兩種布料生產  、
、 兩種型號的時裝共
兩種型號的時裝共 套。已知做一套
套。已知做一套 型號的時裝需用
型號的時裝需用 種布料
種布料 ,
, 種布料
種布料 ,可獲利潤
,可獲利潤 元;做一套
元;做一套 型號的時裝需用
型號的時裝需用 種布料
種布料 ,
, 種布料
種布料 ,可獲利潤
,可獲利潤 元。若設生產
元。若設生產 型號的時裝套數為
型號的時裝套數為 ,用這批布料生產這兩種型號的時裝所獲得的總利潤為
,用這批布料生產這兩種型號的時裝所獲得的總利潤為 元。
元。 (元)與
(元)與 (套)的函數關系,利用一次函數性質,選出(1)中哪個方案所獲利潤最大?最大利潤是多少?
(套)的函數關系,利用一次函數性質,選出(1)中哪個方案所獲利潤最大?最大利潤是多少?查看答案和解析>>
湖北省互聯(lián)網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com