
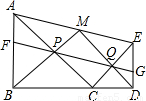
 BD,則∠BMD=90°,判斷①正確;
BD,則∠BMD=90°,判斷①正確; AE,又AF∥EG,根據兩組對邊分別平行的四邊形是平行四邊形可判斷②正確;
AE,又AF∥EG,根據兩組對邊分別平行的四邊形是平行四邊形可判斷②正確; AE,則FP+GQ=
AE,則FP+GQ= AE=PQ,判斷③正確;
AE=PQ,判斷③正確;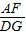 =
= ,同理△BPF∽△EQG,
,同理△BPF∽△EQG,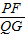 =
=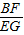 ,則
,則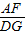 =
= ,AF•EG=BF•DG,又AF=EG,判斷④正確.
,AF•EG=BF•DG,又AF=EG,判斷④正確.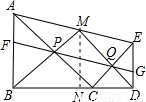 解:①過點M作MN⊥BD,垂足為N,則MN∥DE∥AB,
解:①過點M作MN⊥BD,垂足為N,則MN∥DE∥AB, (AB+ED)=
(AB+ED)= (BC+CD)=
(BC+CD)= BD=BN=ND,
BD=BN=ND, AE,
AE, AE,
AE, AE=
AE= AE=PQ,
AE=PQ,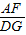 =
=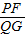 ,
,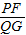 =
= ,
, =
=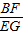 ,
,

 浙大優學小學年級銜接導與練浙江大學出版社系列答案
浙大優學小學年級銜接導與練浙江大學出版社系列答案 小學暑假作業東南大學出版社系列答案
小學暑假作業東南大學出版社系列答案 津橋教育暑假拔高銜接廣東人民出版社系列答案
津橋教育暑假拔高銜接廣東人民出版社系列答案 波波熊暑假作業江西人民出版社系列答案
波波熊暑假作業江西人民出版社系列答案科目:初中數學 來源: 題型:

| BG | CG |
查看答案和解析>>
科目:初中數學 來源: 題型:
 10、如圖,△ABC和△ADE都是等腰直角三角形,∠ACB和∠AED都是直角,點C在AD上,如果△ABC經旋轉后能與△ADE重合,那么點
10、如圖,△ABC和△ADE都是等腰直角三角形,∠ACB和∠AED都是直角,點C在AD上,如果△ABC經旋轉后能與△ADE重合,那么點查看答案和解析>>
科目:初中數學 來源: 題型:
 如圖,△ABC和△CDE均為等腰直角三角形,點B,C,D在一條直線上,點M是AE的中點,BC=3,CD=1.
如圖,△ABC和△CDE均為等腰直角三角形,點B,C,D在一條直線上,點M是AE的中點,BC=3,CD=1.| BC | CD |
查看答案和解析>>
科目:初中數學 來源: 題型:
 如圖,△ABC和△ADE都是等腰直角三角形,∠BAC=∠DAE=90°,四邊形ACDE是平行四邊形,連接CE交AD于點F,連接BD交 CE于點G,連接BE.下列結論中:
如圖,△ABC和△ADE都是等腰直角三角形,∠BAC=∠DAE=90°,四邊形ACDE是平行四邊形,連接CE交AD于點F,連接BD交 CE于點G,連接BE.下列結論中:查看答案和解析>>
科目:初中數學 來源: 題型:
 如圖,△ABC和△ADE都是等腰直角三角形,AB=AC,AD=AE,∠BAC=∠DAE=90°.
如圖,△ABC和△ADE都是等腰直角三角形,AB=AC,AD=AE,∠BAC=∠DAE=90°.| 2 |
| 10 |
| 10 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com