Question

1．如圖，拋物線y=-$\frac{1}{2}$（x+1）（x-2k）（k＞0）交x軸于A、B（A左B右），交y軸于點C，點D在第一象限拋物線的圖象上，且∠ABD=45°，△BCD的面積為$\frac{15}{2}$．
（1）求拋物線解析式；
（2）點P為第一象限拋物線的圖象上一點，過點P作PH⊥x軸，垂足為H，PH交BD于E．把△PAH沿PH翻折，點A落在BH邊上F點，設PF交BD于G，若EG=BG，求點P的坐標；
（3）在（2）的條件下，設PF交拋物線于N，連接AN，Q在線段AN上，若∠PQG=2∠APQ．求點Q的坐標．

Answer 1

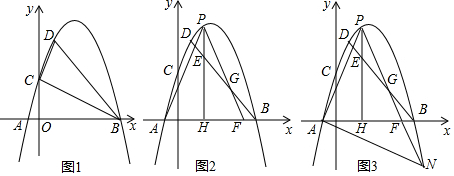
分析 （1）根據(jù)正切函數(shù)，可得D點坐標，根據(jù)面積的和差，可得關于k的方程，根據(jù)解方程，可得答案；
（2）根據(jù)正切值相等，可得關于m的方程，根據(jù)解方程，可得m的值，可得P點坐標；
（3）根據(jù)互余兩角的正切值互為倒數(shù)，可得∠PAN=90°，根據(jù)全等三角形的判定與性質，可得AM，LM，根據(jù)解方程組，可得答案．

解答 解：（1）如圖1，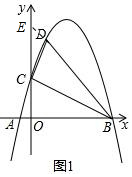
在y=-$\frac{1}{2}$（x+1）（x-2k），當x=0時，y=k，所以C（0，k），
當y=0時，x=-1，或x=2k，所以A（-1，0），B（2k，0），
設BD交y軸于E，所以E（0，2k），設D點坐標為[x，-$\frac{1}{2}$（x+1）（x-2k）]
tan∠ABD=tan45°=$\frac{-\frac{1}{2}（x+1）（x-2k）}{2k-x}$=$\frac{1}{2}$（x+1）=1，
∴x=1
∴D（1，2k-1）
S_△BCD=S_△BCE-S_△DCE=$\frac{1}{2}$k（2k-1）=$\frac{15}{2}$，
解得k₁=3，k₂=-$\frac{5}{2}$（舍）
∴拋物線解析式為：y=-$\frac{1}{2}$（x+1）（x-6）；
（2）如圖2，
作GW⊥AB于W，
∵P點在拋物線上，
∴設P[m，-$\frac{1}{2}$（m+1）（m-6）]
則t an∠PAH=$\frac{PH}{AH}$=$\frac{-\frac{1}{2}（m+1）（m-6）}{m+1}$=-$\frac{1}{2}$（m-6），
因G是BE中點，則GW=HW=$\frac{1}{2}$（6-m），所以WF=WB-BF=$\frac{3}{2}$m-2
tan∠PFA=$\frac{GW}{WF}$=$\frac{\frac{1}{2}（6-m）}{\frac{3}{2}m-2}$=$\frac{6-m}{3m-4}$=-$\frac{1}{2}$（m-6），
因m≠6，解得m=2，
∴P（2，6）；
（3）如圖3，
延長GH、PA交于點L，過L作LM⊥x軸于點M，
∴∠LMA=90°
由（2）可求G（4，2）
∴直線PG解析式為：y=-2x+10，與拋物線聯(lián)立求得N點坐標為（7，4）
tan∠NAB=$\frac{1}{2}$，
∵tan∠PAB=2，
∴∠PAN=90°．
∠PQA=90°-∠APQ，
∵∠PQG=2∠APQ，
∴∠AQL=90°-∠APQ．
在△APQ和△ALQ中，
$\left\{\begin{array}{l}{∠PAQ=∠LAQ=90°}\\{AQ=AQ}\\{∠PQA=∠LQA}\end{array}\right.$
∴△APQ≌△ALQ（ASA）
∴AP=AL．
在△PHA和△LMA中，
$\left\{\begin{array}{l}{∠PHA=∠LMA}\\{∠PAH=∠LAM}\\{PA=LA}\end{array}\right.$，
∴△PHA≌△LMA（AAS）
∴AM=AH=3   LM=PH=6，
∴L（-4，6），
直線GL解析式為：y=x-2    直線AN解析式為：y=-$\frac{1}{2}$x-$\frac{1}{2}$，
聯(lián)立方程組$\left\{\begin{array}{l}{y=x-2}\\{y=-\frac{1}{2}x-\frac{1}{2}}\end{array}\right.$，
解得 Q（1，-1）．

點評 本題考查了二次函數(shù)綜合題，（1）利用正切值得出D點坐標是解題關鍵；（2）利用正切值得出關于m的方程值是解題關鍵；（3）利用全等三角形的判定與性質得出AM，LM是解題關鍵．