
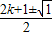 ,即x1=k,x2=k+1,
,即x1=k,x2=k+1,

 新課標快樂提優暑假作業陜西旅游出版社系列答案
新課標快樂提優暑假作業陜西旅游出版社系列答案 暑假銜接培優教材浙江工商大學出版社系列答案
暑假銜接培優教材浙江工商大學出版社系列答案科目:初中數學 來源:第23章《一元二次方程》中考題集(23):23.3 實踐與探索(解析版) 題型:解答題
 .
.查看答案和解析>>
科目:初中數學 來源:2007年全國中考數學試題匯編《一元二次方程》(04)(解析版) 題型:解答題
 .
.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com