
【題目】如圖,![]() ,
,![]() ,以
,以![]() 為直徑作半圓,圓心為
為直徑作半圓,圓心為![]() .以點(diǎn)
.以點(diǎn)![]() 為圓心,
為圓心,![]() 為半徑作弧
為半徑作弧![]() ,過點(diǎn)
,過點(diǎn)![]() 作
作![]() 的平行線交兩弧于點(diǎn)
的平行線交兩弧于點(diǎn)![]() 、
、![]() ,則陰影部分的面積是( )
,則陰影部分的面積是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】A
【解析】
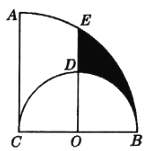
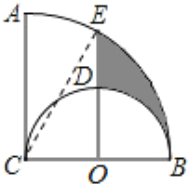
如圖,連接CE.圖中S陰影=S扇形BCE-S扇形BOD-S△OCE.根據(jù)已知條件易求得OB=OC=OD=1,BC=CE=2.∠ECB=60°,OE=![]() 所以由扇形面積公式、三角形面積公式進(jìn)行解答即可.
所以由扇形面積公式、三角形面積公式進(jìn)行解答即可.
解:如圖,連接CE.
∵AC⊥BC,AC=BC=2,
以BC為直徑作半圓,圓心為點(diǎn)O;
以點(diǎn)C為圓心,BC為半徑作弧AB,
∴∠ACB=90°,OB=OC=OD=1,BC=CE=2.
又∵OE∥AC, ∴∠ACB=∠COE=90°.
∴在Rt△OEC中,OC=1,CE=2,
∴∠CEO=30°,∠ECB=60°,OE=![]() ,
,
∴S陰影=S扇形BCE-S扇形BOD-S△OCE
=![]()
![]()
故選:A.


 閱讀快車系列答案
閱讀快車系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,在平面直角坐標(biāo)系中,直線![]() 與
與![]() 軸、
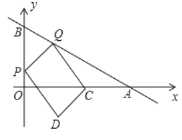
軸、![]() 軸分別角與A、B兩點(diǎn),P、Q分別是線段OB、AB上的兩個(gè)動(dòng)點(diǎn),點(diǎn)P從O出發(fā)一每秒2個(gè)單位長度的速度向終點(diǎn)B運(yùn)動(dòng),同時(shí)Q從B出發(fā),以每秒5個(gè)單位的速度向終點(diǎn)A運(yùn)動(dòng),當(dāng)其中一點(diǎn)到達(dá)終點(diǎn)時(shí)整個(gè)運(yùn)動(dòng)結(jié)束,設(shè)運(yùn)動(dòng)時(shí)間為t秒。
軸分別角與A、B兩點(diǎn),P、Q分別是線段OB、AB上的兩個(gè)動(dòng)點(diǎn),點(diǎn)P從O出發(fā)一每秒2個(gè)單位長度的速度向終點(diǎn)B運(yùn)動(dòng),同時(shí)Q從B出發(fā),以每秒5個(gè)單位的速度向終點(diǎn)A運(yùn)動(dòng),當(dāng)其中一點(diǎn)到達(dá)終點(diǎn)時(shí)整個(gè)運(yùn)動(dòng)結(jié)束,設(shè)運(yùn)動(dòng)時(shí)間為t秒。
(1)求出點(diǎn)Q的坐標(biāo)(用t的代數(shù)式表示)
(2)若C為OA的中點(diǎn),連接PQ、CQ,以PQ、CQ為鄰邊作![]() PQCD.
PQCD.
①是否存在時(shí)間t,使得坐標(biāo)軸切好將![]() PQCD的面積分為1:5的兩個(gè)部分,若存在,求出t的值;若不存在,請說明理由.
PQCD的面積分為1:5的兩個(gè)部分,若存在,求出t的值;若不存在,請說明理由.
②直接寫出整個(gè)運(yùn)動(dòng)過程中![]() PQCD對(duì)角線DQ的取值范圍.
PQCD對(duì)角線DQ的取值范圍.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】已知:正方形![]() 與正方形
與正方形![]() 共頂點(diǎn)
共頂點(diǎn)![]() .
.
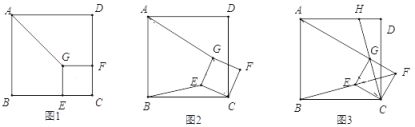
(1)探究:如圖,點(diǎn)![]() 在正方形
在正方形![]() 的邊
的邊![]() 上,點(diǎn)
上,點(diǎn)![]() 在正方形
在正方形![]() 的邊
的邊![]() 上,連接
上,連接![]() .求證:
.求證:![]() ;
;
(2)拓展:將如圖中正方形![]() 繞點(diǎn)
繞點(diǎn)![]() 順時(shí)針方向旋轉(zhuǎn)
順時(shí)針方向旋轉(zhuǎn)![]() 角
角![]() ,如圖所示,試探究線段
,如圖所示,試探究線段![]() 與
與![]() 之間的數(shù)量關(guān)系,并說明理由;
之間的數(shù)量關(guān)系,并說明理由;
(3)運(yùn)用:正方形![]() 在旋轉(zhuǎn)過程中,當(dāng)
在旋轉(zhuǎn)過程中,當(dāng)![]() ,
,![]() ,
,![]() 三點(diǎn)在一條直線上時(shí),如圖所示,延長
三點(diǎn)在一條直線上時(shí),如圖所示,延長![]() 交
交![]() 于點(diǎn)
于點(diǎn)![]() .若
.若![]() ,GH=2
,GH=2![]() ,求
,求![]() 的長.
的長.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
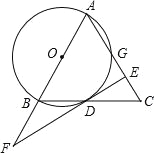
【題目】如圖,在△ABC中,AB=AC,以AB為直徑作⊙O,交BC邊于邊D,交AC邊于點(diǎn)G,過D作⊙O的切線EF,交AB的延長線于點(diǎn)F,交AC于點(diǎn)E.
(1)求證:BD=CD;
(2)若AE=6,BF=4,求⊙O的半徑.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】隨著網(wǎng)絡(luò)購物的盛行,“菜鳥驛站”新興的代收快遞業(yè)務(wù)越來越受到人們的青睞.“菜鳥驛站”某代收點(diǎn)只代收![]() ,
,![]() 兩區(qū)的快遞.4月份該代收點(diǎn)對(duì)
兩區(qū)的快遞.4月份該代收點(diǎn)對(duì)![]() ,
,![]() 兩區(qū)代收數(shù)據(jù)進(jìn)行統(tǒng)計(jì),
兩區(qū)代收數(shù)據(jù)進(jìn)行統(tǒng)計(jì),![]() 區(qū)比
區(qū)比![]() 區(qū)平均每個(gè)快遞輕1千克.
區(qū)平均每個(gè)快遞輕1千克.
(1)4月份第四周![]() 區(qū)共有300個(gè)快遞,
區(qū)共有300個(gè)快遞,![]() 區(qū)快遞數(shù)為
區(qū)快遞數(shù)為![]() 區(qū)的
區(qū)的![]() ,若本周該代收點(diǎn)的快遞重量不低于1700千克,則
,若本周該代收點(diǎn)的快遞重量不低于1700千克,則![]() 區(qū)該周平均每個(gè)快遞至少重多少千克?
區(qū)該周平均每個(gè)快遞至少重多少千克?
(2)隨著夏季的到來,5月份第四周![]() 區(qū)快遞數(shù)比4月份第四周增長了
區(qū)快遞數(shù)比4月份第四周增長了![]() ,但
,但![]() 區(qū)平均每個(gè)快遞比(1)中相應(yīng)最少重量減少了
區(qū)平均每個(gè)快遞比(1)中相應(yīng)最少重量減少了![]() 千克,
千克,![]() 區(qū)快遞數(shù)比4月份第四周增長了10%,平均每單比(1)中相應(yīng)最少重量減少了
區(qū)快遞數(shù)比4月份第四周增長了10%,平均每單比(1)中相應(yīng)最少重量減少了![]() ,第四周兩區(qū)快遞總重量比第四周的最少重量減少了336千克,求
,第四周兩區(qū)快遞總重量比第四周的最少重量減少了336千克,求![]() 的值.
的值.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
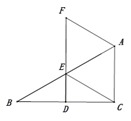
【題目】如圖,在![]() 中,
中,![]() ,點(diǎn)
,點(diǎn)![]() 分別是
分別是![]() 上的中點(diǎn),連接
上的中點(diǎn),連接![]() 并延長至點(diǎn)
并延長至點(diǎn)![]() ,使
,使![]() ,連接
,連接![]() .
.
(1)證明:![]() ;
;
(2)若![]() ,AC=2,連接BF,求BF的長
,AC=2,連接BF,求BF的長
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】二次函數(shù)y=ax2+bx+c(a≠0)的圖象如圖,給出下列四個(gè)結(jié)論:①4ac﹣b2<0;②4a+c<2b;③3b+2c<0;④m(am+b)+b<a(m≠﹣1),其中正確結(jié)論的個(gè)數(shù)是( )
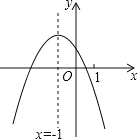
A.4個(gè)B.3個(gè)C.2個(gè)D.1個(gè)
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
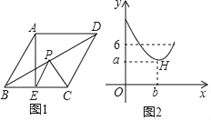
【題目】如圖1,在菱形ABCD中,∠A=120°,點(diǎn)E是BC邊的中點(diǎn),點(diǎn)P是對(duì)角線BD上一動(dòng)點(diǎn),設(shè)PD的長度為x,PE與PC的長度和為y,圖2是y關(guān)于x的函數(shù)圖象,其中H是圖象上的最低點(diǎn),則a+b的值為( )
A.7![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com