
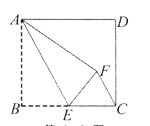
【題目】如圖,正方形紙片![]() 的邊長為5,E是邊
的邊長為5,E是邊![]() 的中點(diǎn),連接
的中點(diǎn),連接![]() .沿
.沿![]() 折疊該紙片,使點(diǎn)B落在F點(diǎn).則
折疊該紙片,使點(diǎn)B落在F點(diǎn).則![]() 的長為______________________.
的長為______________________.
【答案】![]()
【解析】
根據(jù)折疊的性質(zhì)結(jié)合三角形外角的性質(zhì)可證得AE∥FC,利用勾股定理求得![]() 的長,根據(jù)Rt△EBG∽Rt△EAB,即可求得
的長,根據(jù)Rt△EBG∽Rt△EAB,即可求得![]() 的長,根據(jù)三角形中位線的性質(zhì)即可求解.
的長,根據(jù)三角形中位線的性質(zhì)即可求解.
根據(jù)折疊的性質(zhì),△ABE![]() △BFE,AE垂直平分BF,且E是邊BC的中點(diǎn),
△BFE,AE垂直平分BF,且E是邊BC的中點(diǎn),
∴BE=EF=EC,∠BEA=∠FEA,
∴∠EFC=∠ECF,
∵∠BEF =∠BEA+∠FEA=∠EFC+∠ECF,
∴∠BEA=∠ECF,
∴AE∥FC,
∵四邊形![]() 是邊長為5的正方形,且E是邊BC的中點(diǎn),
是邊長為5的正方形,且E是邊BC的中點(diǎn),
∴∠ABC=90![]() ,AB=5,BE=
,AB=5,BE=![]() ,
,
∴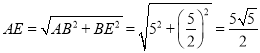 ,
,
連接BF交AE于點(diǎn)G,如圖:

∵AE垂直平分BF,
∴∠BGE=90![]() ,
,
∴Rt△EBG∽Rt△EAB,
∴![]() ,即
,即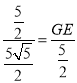 ,
,
∴![]() ,
,
∵GE∥FC,E是邊BC的中點(diǎn),
∴CF=2GE=![]() ,
,
故答案為:![]() .
.


 小學(xué)教材完全解讀系列答案
小學(xué)教材完全解讀系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:
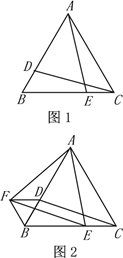
【題目】如圖1,圖2,△ABC是等邊三角形,D、E分別是AB、BC邊上的兩個動點(diǎn)(與點(diǎn)A、B、C不重合),始終保持BD=CE.
(1)當(dāng)點(diǎn)D、E運(yùn)動到如圖1所示的位置時,求證:CD=AE.
(2)把圖1中的△ACE繞著A點(diǎn)順時針旋轉(zhuǎn)60°到△ABF的位置(如圖2),分別連結(jié)DF、EF.
①找出圖中所有的等邊三角形(△ABC除外),并對其中一個給予證明;
②試判斷四邊形CDFE的形狀,并說明理由.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】已知等腰△ABC的頂角∠A=36°(如圖).
(1)請用尺規(guī)作圖法作底角∠ABC的平分線BD,交AC于點(diǎn)D(保留作圖痕跡,不要求寫作法);
(2)證明:△ABC∽△BDC.

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖1,在平面直角坐標(biāo)系中,拋物線y=﹣![]() x+3與x軸的一個交點(diǎn)為點(diǎn)A,與y軸的交點(diǎn)為點(diǎn)B,拋物線的對稱軸l與x軸交于點(diǎn),與線段AB交于點(diǎn)E,點(diǎn)D是對稱軸l上一動點(diǎn).
x+3與x軸的一個交點(diǎn)為點(diǎn)A,與y軸的交點(diǎn)為點(diǎn)B,拋物線的對稱軸l與x軸交于點(diǎn),與線段AB交于點(diǎn)E,點(diǎn)D是對稱軸l上一動點(diǎn).
(1)點(diǎn)A的坐標(biāo)是 ,點(diǎn)B的坐標(biāo)是 ;
(2)是否存在點(diǎn)D,使得△BDE和△ACE相似?若存在,請求出點(diǎn)D的坐標(biāo),若不存在,請說明理由;
(3)如圖2,拋物線的對稱軸l向右平移與線段AB交于點(diǎn)F,與拋物線交于點(diǎn)G,當(dāng)四邊形DEFG是平行四邊形且周長最大時,求出點(diǎn)G的橫坐標(biāo).

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】西安市歷史文化底蘊(yùn)深厚,旅游資源豐富,鐘樓、大雁塔兵馬俑三個景點(diǎn)是人們節(jié)假日游玩的熱門景點(diǎn)
(1)李輝從這三個景點(diǎn)中隨機(jī)選取一個景點(diǎn)去游玩,求他去鐘樓的概率;
(2)張慧、王麗兩名同學(xué),各自從三個景點(diǎn)中隨機(jī)選取一個作為周末游玩的景點(diǎn),用樹狀圖或列表法求他們同時選中大雁塔的概率.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】已知拋物線![]() ,與x軸交于兩點(diǎn)A,B(點(diǎn)A在點(diǎn)B的左側(cè)),與y軸交于點(diǎn)C.
,與x軸交于兩點(diǎn)A,B(點(diǎn)A在點(diǎn)B的左側(cè)),與y軸交于點(diǎn)C.
(Ⅰ)求點(diǎn)A,B和點(diǎn)C的坐標(biāo);
(Ⅱ)已知P是線段![]() 上的一個動點(diǎn).
上的一個動點(diǎn).
①若![]() 軸,交拋物線于點(diǎn)Q,當(dāng)
軸,交拋物線于點(diǎn)Q,當(dāng)![]() 取最大值時,求點(diǎn)P的坐標(biāo);
取最大值時,求點(diǎn)P的坐標(biāo);
②求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】已知如圖,在平面直角坐標(biāo)系xOy中,點(diǎn)A、B、C分別為坐標(biāo)軸上上的三個點(diǎn),且OA=1,OB=3,OC=4,
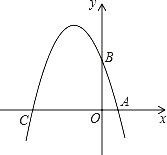
(1)求經(jīng)過A、B、C三點(diǎn)的拋物線的解析式;
(2)在平面直角坐標(biāo)系xOy中是否存在一點(diǎn)P,使得以以點(diǎn)A、B、C、P為頂點(diǎn)的四邊形為菱形?若存在,請求出點(diǎn)P的坐標(biāo);若不存在,請說明理由;
(3)若點(diǎn)M為該拋物線上一動點(diǎn),在(2)的條件下,請求出當(dāng)|PM﹣AM|的最大值時點(diǎn)M的坐標(biāo),并直接寫出|PM﹣AM|的最大值.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,二次函數(shù)![]() (其中
(其中![]() )的圖像與
)的圖像與![]() 軸交于
軸交于![]() 、
、![]() 兩點(diǎn),與
兩點(diǎn),與![]() 軸交于點(diǎn)
軸交于點(diǎn)![]() .
.
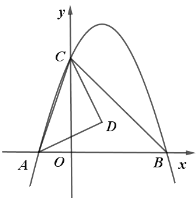
(1)點(diǎn)![]() 的坐標(biāo)為 ,
的坐標(biāo)為 ,![]()
![]() ;
;
(2)若![]() 為
為![]() 的外心,且
的外心,且![]() 與
與![]() 的面積之比為
的面積之比為![]() ,求
,求![]() 的值;
的值;
(3)在(2)的條件下,試探究拋物線![]() 上是否存在點(diǎn)
上是否存在點(diǎn)![]() ,使得
,使得![]() ,若存在,求出點(diǎn)
,若存在,求出點(diǎn)![]() 的坐標(biāo);若不存在,請說明理由.
的坐標(biāo);若不存在,請說明理由.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,在平面直角坐標(biāo)系![]() 中,
中,![]() 的頂點(diǎn)
的頂點(diǎn)![]() ,
,![]() 分別在
分別在![]() ,
,![]() 軸的負(fù)半軸上,
軸的負(fù)半軸上,![]() ,
,![]() 在反比例函數(shù)
在反比例函數(shù)![]() (
(![]() )的圖象上,
)的圖象上,![]() 與
與![]() 軸交于點(diǎn)
軸交于點(diǎn)![]() ,且
,且![]() ,若
,若![]() 的面積是3,則
的面積是3,則![]() 的值是_________.
的值是_________.

查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com