
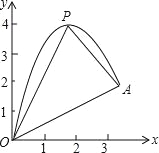
【題目】如圖,一小球從斜坡O點處拋出,球的拋出路線可以用二次函數y=﹣x2+4x刻畫,斜坡可以用一次函數y=![]() x刻畫.
x刻畫.
(1)請用配方法求二次函數圖象的最高點P的坐標;
(2)小球的落點是A,求點A的坐標;
(3)連接拋物線的最高點P與點O、A得△POA,求△POA的面積;
(4)在OA上方的拋物線上存在一點M(M與P不重合),△MOA的面積等于△POA的面積.請直接寫出點M的坐標.
【答案】(1)最高點P的坐標為(2,4);(2)點A的坐標為(![]() ,
,![]() );(3)
);(3)![]() ;(4)點M的坐標為(
;(4)點M的坐標為(![]() ,
,![]() ).
).
【解析】
試題分析:(1)利用配方法拋物線的一般式化為頂點式,即可求出二次函數圖象的最高點P的坐標;
(2)聯立兩解析式,可求出交點A的坐標;
(3)作PQ⊥x軸于點Q,AB⊥x軸于點B.根據S△POA=S△POQ+S△梯形PQBA﹣S△BOA,代入數值計算即可求解;
(4)過P作OA的平行線,交拋物線于點M,連結OM、AM,由于兩平行線之間的距離相等,根據同底等高的兩個三角形面積相等,可得△MOA的面積等于△POA的面積.設直線PM的解析式為y=![]() x+b,將P(2,4)代入,求出直線PM的解析式為y=
x+b,將P(2,4)代入,求出直線PM的解析式為y=![]() x+3.再與拋物線的解析式聯立,得到方程組
x+3.再與拋物線的解析式聯立,得到方程組 ,解方程組即可求出點M的坐標.
,解方程組即可求出點M的坐標.
試題解析:(1)由題意得,y=﹣x2+4x=﹣(x﹣2)2+4,
故二次函數圖象的最高點P的坐標為(2,4);
(2)聯立兩解析式可得: ,解得:
,解得:![]() ,或
,或![]() .
.
故可得點A的坐標為(![]() ,
,![]() );
);
(3)如圖,作PQ⊥x軸于點Q,AB⊥x軸于點B.

S△POA=S△POQ+S△梯形PQBA﹣S△BOA
=![]() ×2×4+
×2×4+![]() ×(
×(![]() +4)×(
+4)×(![]() ﹣2)﹣
﹣2)﹣![]() ×
×![]() ×
×![]()
=4+![]() ﹣
﹣![]()
=![]() ;
;
(4)過P作OA的平行線,交拋物線于點M,連結OM、AM,則△MOA的面積等于△POA的面積.
設直線PM的解析式為y=![]() x+b,
x+b,
∵P的坐標為(2,4),
∴4=![]() ×2+b,解得b=3,
×2+b,解得b=3,
∴直線PM的解析式為y=![]() x+3.
x+3.
由 ,解得
,解得![]() ,
, ,
,
∴點M的坐標為(![]() ,
,![]() ).
).



科目:初中數學 來源: 題型:
【題目】如圖,把四張形狀大小完全相同的小長方形卡片不重疊地放在一個底面為長方形(長為a , 寬為b)的盒子底部,盒子底面未被卡片覆蓋的部分用陰影表示,則這兩塊陰影部分小長方形周長的和為( ) 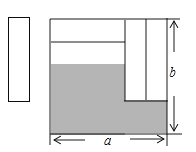
A.a+2b
B.4a
C.4b
D.2a+b
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】今年的“六一”兒童節是個星期五,某校學生會在初一年級進行了學生對學校作息安排的三種期望(全天休息、半天休息、全天上課)的抽樣調查,并把調查結果繪成了下面兩個統計圖,已知此次被調查的男、女學生人數相同.根據圖中信息,下列判斷:①在被調查的學生中,期望全天休息的人數占53%;②本次調查了200名學生;③在被調查的學生中,有30%的女生期望休息半天;④若該校現有初一學生900人,根據調查結果估計期望至少休息半天的學生超過了720人.其中正確的判斷有( ) 

A.4個
B.3個
C.2個
D.1個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知:如圖,四邊形ABCD四條邊上的中點分別為E、F、G、H,順次連接EF、FG、GH、HE,得到四邊形EFGH(即四邊形ABCD的中點四邊形).

(1)四邊形EFGH是什么四邊形?證明你的結論.
(2)當四邊形ABCD的對角線滿足 條件時,四邊形EFGH是矩形;
(3)你學過的哪種特殊四邊形的中點四邊形是矩形? . (填一種即可)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下列四個命題:①若a>b,則a+1>b+1;②若a>b,則a﹣1>b﹣1;③若a>b,則﹣2a<﹣2b;④若a>b,則ac>bc.其中正確的個數是( )
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某調查機構將今年溫州市民最關注的熱點話題分為消費、教育、環保、反腐及其它共五類.根據最近一次隨機調查的相關數據,繪制的統計圖表如下:
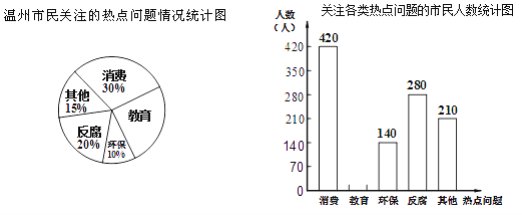
根據以上信息解答下列問題:
(1)本次共調查人________,請在補全條形統計圖并標出相應數據________;
(2)若溫州市約有900萬人口,請你估計最關注教育問題的人數約為多少萬人?
(3)在這次調查中,某單位共有甲、乙、丙、丁四人最關注教育問題,現準備從這四人中隨機抽取兩人進行座談,求抽取的兩人恰好是甲和乙的概率(列樹狀圖或列表說明).
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下列說法正確的是( )
A. 若AB=BC,則點B為線段AC的中點 B. 射線AB和射線BA是同一條射線
C. 兩點之間的線段就是兩點之間的距離 D. 同角的補角一定相等
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com