
 (1)圓內接正六邊形的邊心距為$2\sqrt{3}$,則這個正六邊形的面積為24$\sqrt{3}$cm2.
(1)圓內接正六邊形的邊心距為$2\sqrt{3}$,則這個正六邊形的面積為24$\sqrt{3}$cm2.分析 (1)根據正六邊形的特點,通過中心作邊的垂線,連接半徑,結合解直角三角形的有關知識解決;
(2)過點B作BC⊥水平面于點C,在Rt△ABC中,根據AB=200米,∠A=30°,求出BC的長度即可.
解答 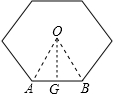 解:(1)如圖,連接OA、OB;過點O作OG⊥AB于點G.
解:(1)如圖,連接OA、OB;過點O作OG⊥AB于點G.
在Rt△AOG中,OG=2$\sqrt{3}$,∠AOG=30°,
∵OG=OA•cos30°,
∴OA=$\frac{OG}{cos30°}$=$\frac{2\sqrt{3}}{\frac{\sqrt{3}}{2}}$=4,
∴這個正六邊形的面積為6×$\frac{1}{2}$×4×2$\sqrt{3}$=24$\sqrt{3}$.
故答案為:24$\sqrt{3}$; (2)過點B作BC⊥水平面于點C,
(2)過點B作BC⊥水平面于點C,
在Rt△ABC中,
∵AB=2000米,∠A=30°,
∴BC=ABsin30°=2000×$\frac{1}{2}$=1000(米).
故答案為1000.
點評 本題考查了解直角三角形的應用-坡度坡角問題,解答本題的關鍵是根據坡角構造直角三角形,利用三角函數的知識進行求解.也考查了正多邊形和圓.


科目:初中數學 來源: 題型:選擇題
 如圖,是直立在高速公路邊水平地面上的交通警示牌,經測量得到如下數據:AM=4米,AB=8米,∠MAD=45°,∠MBC=30°,則警示牌的高CD為( )
如圖,是直立在高速公路邊水平地面上的交通警示牌,經測量得到如下數據:AM=4米,AB=8米,∠MAD=45°,∠MBC=30°,則警示牌的高CD為( )| A. | 4$\sqrt{3}$米 | B. | (2$\sqrt{3}$+2)米 | C. | (4$\sqrt{2}$-4)米 | D. | (4$\sqrt{3}$-4)米 |
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
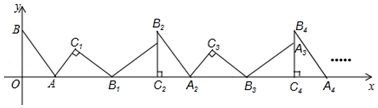
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 不經過點A | B. | 不經過點B | ||
| C. | 開口向下 | D. | 頂點為(2.5,-0.125) |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com