已知函數y1=x,y2=x2+mx+n,x1、x2是方程y1=y2的兩個實根,點P(s,t)在函數y2的圖象上.
(1)若x1=2,x2=4,求m,n的值;
(2)在(1)的條件下,當0≤s≤6時,求t的取值范圍;
(3)當0<x1<x2<1,0<s<1時,試確定t,x1,x2三者之間的大小關系.
【答案】
分析:(1)通過把x
1=2,x
2=4分別代入y
1=y
2,確定m,n的值即可;
(2)首先根據二次函數的對稱軸得出s=

,再利用當0≤s≤

時,當

<s≤6時,分別求出t的取值范圍即可;
(3)利用t-x
1=s
2+ms-x
12-mx
1=(s-x
1)(s+x
1+m),t-x
2=s
2+ms-x
22-mx
2=(s-x
2)(s+x
2+m),結合當0<s≤x
1時,當x
1<s≤x
2時,當x
2<s<1時分別求出t,x
1,x
2三者之間的大小關系即可.
解答:解:(1)∵y
1=x,y
2=x
2+mx+n,y
1=y
2,
∴x
2+(m-1)x+n=0.將x
1=2,x
2=4分別代入x
2+(m-1)x+n=0,
得
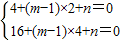
,
解得:
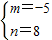
.
(2)由(1)知,y
2=x
2-5x+8=(x-

)
2+

,
∵點P(s,t)在函數y
2的圖象上,
∴t=(s-

)
2+

,
當0≤s≤

時,
當s=0,t=8,當s=

,t=

,
則

≤t≤8,
當

<s≤6時,
當s=

,t=

,當s=6,t=14,
則

<t≤14,
(3)由已知,得x
1=x
12+mx
1+n,x
2=x
22+mx
2+n,t=s
2+ms+n.
t-x
1=s
2+ms-x
12-mx
1=(s-x
1)(s+x
1+m),
t-x
2=s
2+ms-x
22-mx
2=(s-x
2)(s+x
2+m),
x
1-x
2=(x
12+mx
1+n)-(x
22+mx
2+n)
∴x
1-x
2=(x
1-x
2)(x
1+x
2+m),
∴(x
1-x
2)(x
1+x
2+m-1)=0,
∵0<x
1<x
2<1,∴x
1-x
2≠0,
∴x
1+x
2+m-1=0,
有x
1+m=1-x
2>0,
又∵0<s<1,
∴s+x
1+m>0,s+x
2+m>0,
∴當0<s≤x
1時,t≤x
1<x
2,
當x
1<s≤x
2時,x
1<t≤x
2,
當x
2<s<1時,x
1<x
2<t.
點評:本題主要考查了一元二次方程與一次函數及二次函數的相關知識,一元二次方程與函數相結合的綜合問題是初中與高中知識銜接的重點內容.對于這類問題,通常需要學生熟悉掌握方程與函數的概念與性質及兩者之間的聯系.

 ,再利用當0≤s≤
,再利用當0≤s≤ 時,當
時,當 <s≤6時,分別求出t的取值范圍即可;
<s≤6時,分別求出t的取值范圍即可;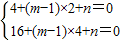 ,
,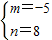 .
. )2+
)2+ ,
, )2+
)2+ ,
, 時,
時, ,t=
,t= ,
, ≤t≤8,
≤t≤8, <s≤6時,
<s≤6時, ,t=
,t= ,當s=6,t=14,
,當s=6,t=14, <t≤14,
<t≤14,

 已知函數y1=x-1和y2=
已知函數y1=x-1和y2= 已知函數y1=x+2,y2=-2x+8
已知函數y1=x+2,y2=-2x+8