(1)證明:∵AB∥DC,
∴∠FCE=∠ABE,∠CFE=∠BAE.
又E是BC的中點,
∴△ABE≌△FCE.
∴AB=CF.
(2)解:梯形ABCD應滿足∠ADC=90°,CD=

BC.
理由如下:
∵AB∥CF,AB=CF,
∴四邊形ABFC是平行四邊形.
要使它成為菱形,只需AF⊥BC.
根據將梯形沿對角線AC折疊恰好D點與E點重合,得
∠ADC=90°,CD=

BC.
(3)解:∵四邊形ABFC為菱形,
∴AC=CF.
∴∠CAF=∠AFC.
∴∠ACD=∠CAF+∠AFC=2∠CAF.
由于是折疊,得∠CAD=∠CAF.
∴∠ACD=2∠CAD.
又∠ADC=90°,
∴∠CAF=∠CAD=30°.
∴sin∠CAF=

.
分析:(1)根據AAS或ASA可以證明△ABE≌△FCE,從而證明AB=CF;
(2)根據(1)的結論,知四邊形ABFC是平行四邊形,要使它成為菱形,則需AF⊥BC于E.結合折疊的方法,則∠ADC=∠AEC=90°,CD=

BC;
(3)根據四邊形ABFC為菱形,得AC=CF,則∠CAF=∠AFC;根據三角形的外角的性質,得∠ACD=2∠CAF;根據折疊,得∠CAD=∠CAF,則∠ACD=2∠CAD,從而求得∠CAF=30°,進而求其正弦值.
點評:此題綜合運用了全等三角形的判定及性質、菱形的判定及性質、等腰三角形的性質、三角形的外角的性質以及折疊的性質.

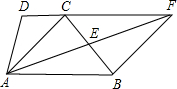 BF.
BF. BC.
BC. BC.
BC. .
. BC;
BC;

