
【題目】如圖1,在平面直角坐標系中,拋物線y=ax2+bx+3(a≠0)與x軸分別交于A(﹣3,0),B兩點,與y軸交于點C,拋物線的頂點E(﹣1,4),對稱軸交x軸于點F.
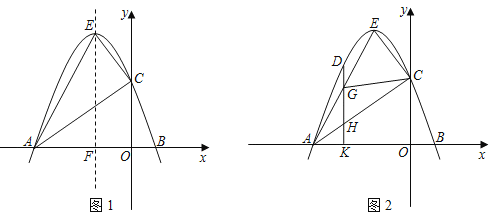
(1)請直接寫出這條拋物線和直線AE、直線AC的解析式;
(2)連接AC、AE、CE,判斷△ACE的形狀,并說明理由;
(3)如圖2,點D是拋物線上一動點,它的橫坐標為m,且﹣3<m<﹣1,過點D作DK⊥x軸于點K,DK分別交線段AE、AC于點G、H.在點D的運動過程中,
①DG、GH、HK這三條線段能否相等?若相等,請求出點D的坐標;若不相等,請說明理由;
②在①的條件下,判斷CG與AE的數量關系,并直接寫出結論.
【答案】(1)y=﹣x2﹣2x+3;y=2x+6,y=x+3;(2)直角三角形,見解析;(3)①相等,(﹣2,3);②AE=2CG
【解析】
(1)設頂點式,將A點坐標代入,再化為一般式,根據常數項等于3即可求出a的值,由此可得拋物線解析式,設直線AE和AC的解析式,再分別將A點、E點代入即可求出直線AE的解析式,將A點、C點代入即可求出直線AC解析式;
(2)分別求出AC2,CE2,AE2,利用勾股定理的逆定理即可判定;
(3)①設出點D、G、H的坐標,表示DG、HK、GH長度,先根據DG=HK列出方程求得x值,再據此求得DG、HK、GH長度,即可得解;②分別求出CG和AE的長度,即可得出它們的數量關系.
解:(1)拋物線的表達式為:y=a(x+1)2+4=ax2+2ax+a+4,
故a+4=3,解得:a=﹣1,
故拋物線的表達式為:y=﹣x2﹣2x+3;
設直線AE的解析式為:![]() ,
,
將點A(﹣3,0)、E(﹣1,4)的坐標代入一次函數表達式得
![]() ,
,
解得:![]() ,
,
故直線AE的表達式為:y=2x+6,
設直線AC的解析式為:![]() ,
,
將點A(﹣3,0)、C(0,3)的坐標代入一次函數表達式得
![]() ,
,
解得:![]() ,
,
故直線AC的表達式為:y=x+3;
(2)點A、C、E的坐標分別為:(﹣3,0)、(0,3)、(﹣1,4),
則AC2=![]() =18,CE2=
=18,CE2=![]() =2,AE2=
=2,AE2=![]() =20,
=20,
故AC2+CE2=AE2,則△ACE為直角三角形;
(3)①設點D、G、H的坐標分別為:(x,﹣x2﹣2x+3)、(x,2x+6)、(x,x+3),
DG=﹣x2﹣2x+3﹣2x﹣6=﹣x2﹣4x﹣3;HK=x+3;GH=2x+6﹣x﹣3=x+3;
當DG=HK時,﹣x2﹣4x﹣3=x+3,解得:x=﹣2或﹣3(舍去﹣3),故x=﹣2,
當x=﹣2時,DG=HK=GH=1,
故DG、GH、HK這三條線段相等時,點D的坐標為:(﹣2,3);
②由①的點G的坐標為:(﹣2,2)
CG=![]() =
=![]() ;AE=
;AE=![]() =2
=2![]() ,
,
故AE=2CG.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
【題目】如圖①,四邊形![]() 是知形,
是知形,![]() ,點
,點![]() 是線段
是線段![]() 上一動點(不與
上一動點(不與![]() 重合),點
重合),點![]() 是線段
是線段![]() 延長線上一動點,連接
延長線上一動點,連接![]() 交
交![]() 于點
于點![]() .設
.設![]() ,已知
,已知![]() 與
與![]() 之間的函數關系如圖②所示.
之間的函數關系如圖②所示.
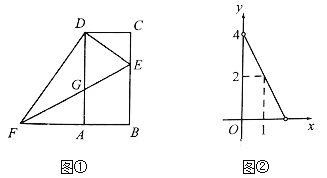
(1)求圖②中![]() 與
與![]() 的函數表達式;
的函數表達式;
(2)求證:![]() ;
;
(3)是否存在![]() 的值,使得
的值,使得![]() 是等腰三角形?如果存在,求出
是等腰三角形?如果存在,求出![]() 的值;如果不存在,說明理由
的值;如果不存在,說明理由
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】二次函數![]() (
(![]() ,
,![]() ,
,![]() 為常數,且
為常數,且![]() )中的
)中的![]() 與
與![]() 的部分對應值如下表:
的部分對應值如下表:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
以下結論:
①二次函數![]() 有最小值為
有最小值為![]() ;
;
②當![]() 時,
時,![]() 隨
隨![]() 的增大而增大;
的增大而增大;
③二次函數![]() 的圖象與
的圖象與![]() 軸只有一個交點;
軸只有一個交點;
④當![]() 時,
時,![]() .
.
其中正確的結論有( )個
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
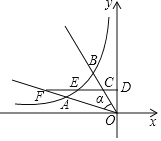
【題目】如圖,角α的兩邊與雙曲線y=![]() (k<0,x<0)交于A、B兩點,在OB上取點C,作CD⊥y軸于點D,分別交雙曲線y=
(k<0,x<0)交于A、B兩點,在OB上取點C,作CD⊥y軸于點D,分別交雙曲線y=![]() 、射線OA于點E、F,若OA=2AF,OC=2CB,則
、射線OA于點E、F,若OA=2AF,OC=2CB,則![]() 的值為______.
的值為______.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,平面直角坐標系中,一次函數y=﹣x+b的圖象與反比例函數y=﹣![]() 在第二象限內的圖象相交于點A,與x軸的負半軸交于點B,與y軸的負半軸交于點C.
在第二象限內的圖象相交于點A,與x軸的負半軸交于點B,與y軸的負半軸交于點C.
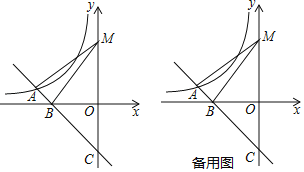
(1)求∠BCO的度數;
(2)若y軸上一點M的縱坐標是4,且AM=BM,求點A的坐標;
(3)在(2)的條件下,若點P在y軸上,點Q是平面直角坐標系中的一點,當以點A、M、P、Q為頂點的四邊形是菱形時,請直接寫出點Q的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某企業設計了一款工藝品,每件的成本是50元,為了合理定價,投放市場進行試銷.據市場調查,銷售單價是100元時,每天的銷售量是50件,而銷售單價每降低1元,每天就可多售出5件,但要求銷售單價不得低于成本.
(1)當銷售單價為70元時,每天的銷售利潤是多少?
(2)求出每天的銷售利潤y(元)與銷售單價x(元)之間的函數關系式,并求出自變量![]() 的取值范圍;
的取值范圍;
(3)如果該企業每天的總成本不超過7000元,那么銷售單價為多少元時,每天的銷售利潤最大?最大利潤是多少?(每天的總成本=每件的成本×每天的銷售量)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,活動課上,小玥想要利用所學的數學知識測量某個建筑地所在山坡AE的高度,她先在山腳下的點E處測得山頂A的仰角是30°,然后,她沿著坡度i=1:1的斜坡按速度20米/分步行15分鐘到達C處,此時,測得點A的俯角是15°.圖中點A、B、E、D、C在同一平面內,且點D、E、B在同一水平直線上,求出建筑地所在山坡AE的高度AB.(精確到0.1米,參考數據:![]() ≈1.41).
≈1.41).

查看答案和解析>>
科目:初中數學 來源: 題型:
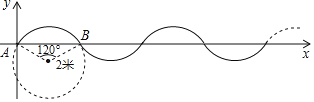
【題目】如圖,在單位長度為1米的平面直角坐標系中,曲線是由半徑為2米,圓心角為120°圓弧多次復制并首尾連接而成,現有一點P從A(A為坐標原點),以每秒![]() 米的速度沿曲線向右運動,則在第2020秒時點P的縱坐標為_____.
米的速度沿曲線向右運動,則在第2020秒時點P的縱坐標為_____.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】合肥百大集團新進了40臺空調機,60臺電冰箱,計劃調配給下屬的甲、乙兩個連鎖店銷售,其中70臺給甲連鎖店,30臺給乙連鎖店.兩個連鎖店銷售這兩種電器每臺的利潤(元)如下表:
空調機 | 電冰箱 | |
甲連鎖店 | 200 | 170 |
乙連鎖店 | 160 | 150 |
設集團調配給甲連鎖店x臺空調機,集團賣出這100臺電器的總利潤為y(元).
(1)求y關于x的函數關系式,并求出x的取值范圍;
(2)為了促銷,集團決定僅對甲連鎖店的空調機每臺讓利a元銷售,其他的銷售利潤不變,并且讓利后每臺空調機的利潤仍然高于甲連鎖店銷售的每臺電冰箱的利潤,問該集團應該如何設計調配方案,才能使總利潤達到最大?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com