Question

11．如圖，將等腰Rt△GAE繞點(diǎn)A順時(shí)針旋轉(zhuǎn)60°得到△DAB，其中∠GAE=∠DAB=90°，GE與AD交于點(diǎn)M，過點(diǎn)D作DC∥AB交AE于點(diǎn)C．已知AF平分∠GAM，EH⊥AE交DC于點(diǎn)H，連接FH交DM于點(diǎn)N，若AC=2$\sqrt{3}$，則MN的值為9-5$\sqrt{3}$．

Answer 1

分析 作MK⊥AC，F(xiàn)T⊥AD垂足分別為K，T，證明△AGF≌△AEM，△AFT≌△AMK得到AF=AM，F(xiàn)T=MK=EK=DM，在RT△ADC中根據(jù)已知條件求出CD，AD，設(shè)MK=EK=x，根據(jù)AE=AK+EK列出方程求出x，在RT△HEC中求出HC，進(jìn)而求出DH，再根據(jù)$\frac{DH}{FT}=\frac{DN}{NT}$，求出DN，利用MN=AD-AM-DN求出MN．

解答 解：作MK⊥AC，F(xiàn)T⊥AD垂足分別為K，T，
∵Rt△GAE繞點(diǎn)A順時(shí)針旋轉(zhuǎn)60°得到△DAB，
∴∠GAD=∠CAB=60°，
∵∠GAE=∠DAB=90°，AG=AE=AD=AB，
∴∠DAC=30°，∠G=∠AEG=45°，
∵AF平分∠GAD，
∴∠GAF=∠FAT=30°，
在△AGF和△AEM中，
$\left\{\begin{array}{l}{∠G=∠AEM}\\{AG=AE}\\{∠GAF=∠MAE}\end{array}\right.$，
∴△AGF≌△AEM，
∴AF=AM
在△AFT和△AMK中，
$\left\{\begin{array}{l}{∠FAT=∠MAK}\\{∠FTA=∠MKA}\\{AF=AM}\end{array}\right.$，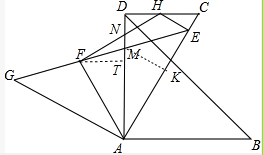
∴△AFT≌△AMK，
∴AT=AK，
∵AD=AE，
∴DT=EK，
∵∠KME=∠KEM=45°，
∴MK=EK=DT=FT，
設(shè)MK=KE=x，則AK=$\sqrt{3}$x，
∵$AC=2\sqrt{3}$，∠DAC=30°，
∴$DC=\sqrt{3}$，AD=3，∴AE=AD=3，
∴x+$\sqrt{3}$x=3
x=$\frac{3（\sqrt{3}-1）}{2}$，
∴DT=FT=MK=EK=$\frac{3（\sqrt{3}-1）}{2}$，AM=3（$\sqrt{3}$-1），EC=2$\sqrt{3}$-3，
在RT△HEC中，∵∠C=60°，EC=2$\sqrt{3}$-3，
∴HC=2EC=4$\sqrt{3}$-6，DH=DC-HC=$\sqrt{3}$-（4$\sqrt{3}$-6）=6-3$\sqrt{3}$，
設(shè)DN=y，∵DH∥FT，
∴$\frac{DH}{FT}=\frac{DN}{NT}$，
∴$\frac{6-3\sqrt{3}}{\frac{3（\sqrt{3}-1）}{2}}=\frac{y}{\frac{3（\sqrt{3}-1）}{2}-y}$，
∴y=2$\sqrt{3}$-3，
∴MN=AD-AM-DN=3-3（$\sqrt{3}$-1）-（2$\sqrt{3}$-3）=9-5$\sqrt{3}$．

點(diǎn)評(píng) 本題考查旋轉(zhuǎn)性質(zhì)、全等三角形的判定和性質(zhì)、勾股定理、平行成比例等知識(shí)，靈活運(yùn)用全等三角形的性質(zhì)是解題的關(guān)鍵．