【題目】如圖所示，在折線ABCDEFG中，已知∠1=∠2=∠3=∠4=∠5，延長AB，GF交于點M．試探索∠AMG與∠3的關系，并說明理由．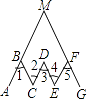 
【答案】解：∠AMG=∠3．理由如下： ∵∠2=∠3，
∴BC∥DE，
∵∠4=∠5，
∴DE∥FG，
∴BC∥FG，
∴∠1=∠AMG，
而∠1=∠3，
∴∠AMG=∠3．
【解析】根據(jù)平行線的判定由∠2=∠3得到BC∥DE，由∠4=∠5得到DE∥FG，則BC∥FG，根據(jù)平行線的性質得∠1=∠AMG，∠1=∠3，則∠AMG=∠3．
【考點精析】關于本題考查的平行線的判定與性質，需要了解由角的相等或互補（數(shù)量關系）的條件，得到兩條直線平行（位置關系）這是平行線的判定；由平行線（位置關系）得到有關角相等或互補（數(shù)量關系）的結論是平行線的性質才能得出正確答案．
科目：初中數(shù)學 來源： 題型：
【題目】如果兩個數(shù)的和是負數(shù)，那么這兩個數(shù)（ ）
A.同是正數(shù)
B.同為負數(shù)
C.至少有一個為正數(shù)
D.至少有一個為負數(shù)
查看答案和解析>>
科目：初中數(shù)學 來源： 題型：
【題目】已知： 
=8，則點A（1，a）關于y軸的對稱點為點B，將點B向下平移2個單位后，再向左平移3個單位得到點C，則C點與原點及A點所圍成的三角形的面積為多少？
查看答案和解析>>
科目：初中數(shù)學 來源： 題型：
【題目】去年“雙11”購物節(jié)的快遞量暴增，某快遞公司要在街道旁設立一個派送還點，向A，B兩居民區(qū)投送快遞，派送點應該設在什么地方，才能使它到A，B的距離之和最短？快遞員根據(jù)實際情況，以街道為x軸，建立了如圖所示的平面直角坐標系，測得坐標A（﹣2，2）、B（6，4），則派送點的坐標是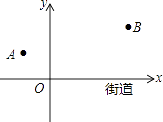 
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com