
【題目】如圖1,點![]() 、
、![]() 、
、![]() 、
、![]() 分別在矩形
分別在矩形![]() 的邊
的邊![]() 、
、![]() 、
、![]() 、
、![]() 上,
上,![]() .
.
求證:![]() .(
.(![]() 表示面積)
表示面積)

實驗探究:
某數學實驗小組發現:若圖1中![]() ,點
,點![]() 在
在![]() 上移動時,上述結論會發生變化,分別過點
上移動時,上述結論會發生變化,分別過點![]() 、
、![]() 作
作![]() 邊的平行線,再分別過點
邊的平行線,再分別過點![]() 、
、![]() 作
作![]() 邊的平行線,四條平行線分別相交于點
邊的平行線,四條平行線分別相交于點![]() 、
、![]() 、
、![]() 、
、![]() ,得到矩形
,得到矩形![]() .
.
如圖2,當![]() 時,若將點
時,若將點![]() 向點
向點![]() 靠近(
靠近(![]() ),經過探索,發現:
),經過探索,發現:
![]() .
.
如圖3,當![]() 時,若將點
時,若將點![]() 向點
向點![]() 靠近(
靠近(![]() ,請探索
,請探索![]() 、
、![]() 與
與![]() 之間的數量關系,并說明理由.
之間的數量關系,并說明理由.

遷移應用:
請直接應用“實驗探究”中發現的結論解答下列問題.
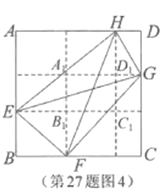
(1)如圖4,點![]() 、
、![]() 、
、![]() 、
、![]() 分別是面積為25的正方形
分別是面積為25的正方形![]() 各邊上的點,已知
各邊上的點,已知![]() ,
,![]() ,
,![]() ,
,![]() ,求
,求![]() 的長.
的長.

(2)如圖5,在矩形![]() 中,
中,![]() ,
,![]() ,點
,點![]() 、
、![]() 分別在邊
分別在邊![]() 、
、![]() 上,
上,![]() ,
,![]() ,點
,點![]() 、
、![]() 分別是邊
分別是邊![]() 、
、![]() 上的動點,且
上的動點,且![]() ,連接
,連接![]() 、
、![]() ,請直接寫出四邊形
,請直接寫出四邊形![]() 面積的最大值.
面積的最大值.

【答案】問題呈現:![]() ;實驗探究:
;實驗探究:![]() ;遷移應用:(1)
;遷移應用:(1)![]() ;(2)
;(2)![]()
【解析】
試題分析:問題呈現:根據矩形的性質,通過割補法利用三角形的面積和矩形的面積可得到結論;
實驗探究:由題意得,當將點![]() 向點
向點![]() 靠近
靠近![]() 時,通過割補法利用三角形的面積和矩形的面積可得到結論;
時,通過割補法利用三角形的面積和矩形的面積可得到結論;
遷移應用:(1)由上面的結論,結合圖形,通過割補法利用三角形的面積和矩形的面積可得到結論;
(2)直接根據規律寫出結果即可.
試題解析:問題呈現:
因為四邊形![]() 是矩形,所以
是矩形,所以![]() ,
,![]() ,
,
又因為![]() ,所以四邊形
,所以四邊形![]() 是矩形,
是矩形,
所以![]() ,同理可得
,同理可得![]() .
.
因為![]() ,所以
,所以![]() .
.
實驗探究:
由題意得,當將點![]() 向點
向點![]() 靠近
靠近![]() 時,
時,
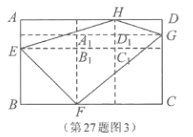
如圖所示,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
所以![]() ,
,
所以![]() ,
,
即![]() .
.
遷移應用:
(1) 如圖所示,由“實驗探究”的結論可知![]() ,
,
所以![]() ,
,
因為正方形面積是25,所以邊長為5,
又![]() ,
,
所以![]() ,
,![]() ,
,
所以![]() ,
,
所以,![]() .
.
(2)四邊形![]() 面積的最大值為
面積的最大值為![]() .
.


科目:初中數學 來源: 題型:
【題目】若A(0,y1),B(﹣3,y2),C(3,y3)為二次函數y=﹣x2+4x﹣k的圖象上的三點,則y1,y2,y3的大小關系是( )
A.y1<y2<y3B.y2<y1<y3C.y3<y1<y2D.y1<y3<y2
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系![]() 中,過點
中,過點![]() 的直線交
的直線交![]() 軸正半軸于點
軸正半軸于點![]() ,將直線
,將直線![]() 繞著點
繞著點![]() 順時針旋轉
順時針旋轉![]() 后,分別與
后,分別與![]() 軸
軸![]() 軸交于點
軸交于點![]() 、
、![]() .
.
(1)若![]() ,求直線
,求直線![]() 的函數關系式;
的函數關系式;
(2)連接![]() ,若
,若![]() 的面積是5,求點
的面積是5,求點![]() 的運動路徑長.
的運動路徑長.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某縣響應“建設環保節約型社會”的號召,決定資助部分村鎮修建一批沼氣池,使農民用到經濟、環保的沼氣能源.幸福村共有264戶村民,政府補助村里34萬元,不足部分由村民集資.修建A型、B型沼氣池共20個.兩種型號沼氣池每個修建費用、可供使用戶數、修建用地情況如下表:
沼氣池 | 修建費用(萬元/個) | 可供使用戶數(戶/個) | 占地面積(m2/個) |
A型 | 3 | 20 | 48 |
B型 | 2 | 3 | 6 |
政府相關部門批給該村沼氣池修建用地708平方米.設修建A型沼氣池x個,修建兩種型號沼氣池共需費用y萬元.
(1)用含有x的代數式表示y;
(2)不超過政府批給修建沼氣池用地面積,又要使該村每戶村民用上沼氣的修建方案有幾種;
(3)若平均每戶村民集資700元,能否滿足所需費用最少的修建方案.
查看答案和解析>>
科目:初中數學 來源: 題型:
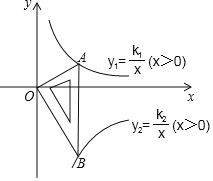
【題目】如圖所示是一塊含30°,60°,90°的直角三角板,直角頂點O位于坐標原點,斜邊AB垂直于x軸,頂點A在函數y1=![]() (x>0)的圖象上,頂點B在函數y2=
(x>0)的圖象上,頂點B在函數y2=![]() (x>0)的圖象上,∠ABO=30°,則
(x>0)的圖象上,∠ABO=30°,則![]() = .
= .
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,圓柱形容器中,高為120cm,底面周長為100cm,在容器內壁離容器底部40cm,的點B處有一蚊子,此時一只壁虎正好在容器外壁,離容器上沿40cm與蚊子相對的點A處,
則壁虎捕捉蚊子的最短距離為Cm(容器厚庋忽略不計).
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com