
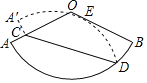
【題目】如圖,已知扇形AOB的圓心角為120°,點C是半徑OA上一點,點D是![]() 上一點.將扇形AOB沿CD對折,使得折疊后的圖形恰好與半徑OB相切于點E.若∠OCD=45°,OC=
上一點.將扇形AOB沿CD對折,使得折疊后的圖形恰好與半徑OB相切于點E.若∠OCD=45°,OC=![]() +1,則扇形AOB的半徑長是( )
+1,則扇形AOB的半徑長是( )
A. 2+![]() B. 2+
B. 2+![]() C. 2
C. 2![]() D.
D. ![]()
【答案】B
【解析】
作O關于CD的對稱點F,連接CF、EF,則EF為扇形AOB的半徑,由折疊的性質得:∠FCD=∠OCD=45°,FC=OC=![]() +1,得出△OCF是等腰直角三角形,得出∠COF=45°,OF=
+1,得出△OCF是等腰直角三角形,得出∠COF=45°,OF=![]() OC=
OC=![]() +
+![]() ,∠EOF=∠AOB﹣∠COF=75°,由切線的性質得出∠OEF=90°,得出∠OFE=15°,由三角函數即可得出結果.
,∠EOF=∠AOB﹣∠COF=75°,由切線的性質得出∠OEF=90°,得出∠OFE=15°,由三角函數即可得出結果.
作O關于CD的對稱點F,連接CF、EF,如圖1所示:
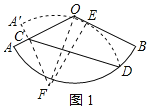
則EF為扇形AOB的半徑,
由折疊的性質得:∠FCD=∠OCD=45°,FC=OC=![]() +1,
+1,
∴∠OCF=90°,
∴△OCF是等腰直角三角形,
∴∠COF=45°,OF=![]() OC=
OC=![]() +
+![]() ,
,
∴∠EOF=∠AOB﹣∠COF=75°,
∵折疊后的圖形恰好與半徑OB相切于點E,
∴∠OEF=90°,
∴∠OFE=15°,
∵cos∠OFE=![]() cos15°=
cos15°=![]() ,
,
如圖2所示:
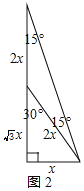
∴EF=OF×cos15°=(![]() +
+![]() )×
)×![]() =2+
=2+![]() ;
;
故選:B.


科目:初中數學 來源: 題型:
【題目】已知:如圖,在梯形ABCD中,AB∥CD,∠D=90°,AD=CD=2,點E在邊AD上(不與點A、D重合),∠CEB=45°,EB與對角線AC相交于點F,設DE=x.
(1)用含x的代數式表示線段CF的長;
(2)如果把△CAE的周長記作C△CAE,△BAF的周長記作C△BAF,設![]() =y,求y關于x的函數關系式,并寫出它的定義域;
=y,求y關于x的函數關系式,并寫出它的定義域;
(3)當∠ABE的正切值是![]() 時,求AB的長.
時,求AB的長.

查看答案和解析>>
科目:初中數學 來源: 題型:
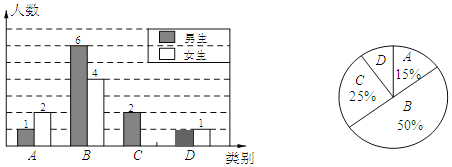
【題目】李老師為了解某校學生完成數學課前預習的具體情況,對部分學生進行了跟蹤調查,并將調查結果分為四類,A:很好;B:較好;C:一般;D:較差.繪制成如下統計圖.
(1)李老師一共調查了多少名同學?并將下面條形統計圖補充完整.
(2)若該校有1000名學生,則數學課前預習“很好”和“較好”總共約多少人?
(3)為了共同進步,李老師想從被調查的A類和D類學生中各隨機選取一位同學進行“一幫一”互助學習,求出所選兩位同學恰好是一位男同學和一位女同學的概率.(要求列表或樹狀圖)
查看答案和解析>>
科目:初中數學 來源: 題型:
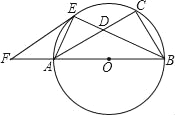
【題目】如圖,已知以Rt△ABC的邊AB為直徑作△ABC的外接圓⊙O,∠B的平分線BE交AC于D,交⊙O于E,過E作EF∥AC交BA的延長線于F.
(1)求證:EF是⊙O切線;
(2)若AB=15,EF=10,求AE的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某市農林種植專家指導貧困戶種植紅梨和青棗,收獲的紅梨和青棗優(yōu)先進入該市水果市場.已知某水果經銷商購進了紅梨和青棗兩種水果各10箱,分配給下屬的甲、乙兩個零售店(分別簡稱甲店、乙店)銷售.預計每箱水果的盈利情況如表
紅梨/箱 | 青棗/箱 | |
甲店 | 22元 | 34元 |
乙店 | 18元 | 26元 |
(1)若甲、乙兩店各配貨10箱,其中甲店配紅梨2箱,青棗8箱;乙店配紅梨8箱,青棗2箱,請你計算出經銷商能盈利多少元?
(2)若甲、乙兩店各配貨10箱,且在保證乙店盈利不小于200元的條件下,請你設計出使水果經銷商盈利最大的配貨方案.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某水果零售商店,通過對市場行情的調查,了解到兩種水果銷路比較好,一種是冰糖橙,一種是睡美人西瓜.通過兩次訂貨購進情況分析發(fā)現,買40箱冰糖橙和15箱睡美人西瓜花去2000元,買20箱冰糖橙和30箱睡美人西瓜花去1900元.
(1)請求出購進這兩種水果每箱的價格是多少元?
(2)該水果零售商在五一期間共購進了這兩種水果200箱,冰糖橙每箱以40元價格出售,西瓜以每箱50元的價格出售,獲得的利潤為w元.設購進的冰糖橙箱數為a箱,求w關于a的函數關系式;
(3)在條件(2)的銷售情況下,但是每種水果進貨箱數不少于30箱,西瓜的箱數不少于冰糖橙箱數的5倍,請你設計進貨方案,并計算出該水果零售商店能獲得的最大利潤是多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
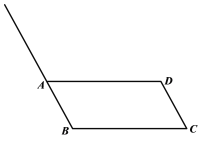
【題目】下面是小東設計的“作平行四邊形一邊中點”的尺規(guī)作圖過程.
已知:平行四邊形ABCD.
求作:點M,使點M為邊AD的中點.

作法:如圖,
①作射線BA;
②以點A為圓心,CD長為半徑畫弧,交BA的延長線于點E;
③連接EC交AD于點M.
所以點M就是所求作的點.
根據小東設計的尺規(guī)作圖過程,
(1)使用直尺和圓規(guī),補全圖形(保留作圖痕跡);
(2)完成下面的證明.
證明:連接AC,ED.
∵四邊形ABCD是平行四邊形,
∴![]() .
.
∵AE= ,
∴四邊形EACD是平行四邊形( )(填推理的依據).
∴![]() ( )(填推理的依據).
( )(填推理的依據).
∴點M為所求作的邊AD的中點.
查看答案和解析>>
科目:初中數學 來源: 題型:
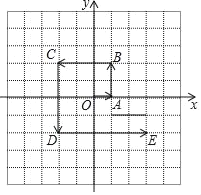
【題目】每個小方格都是邊長為1的正方形,在平面直角坐標系中.
(1)寫出圖中從原點O出發(fā),按箭頭所指方向先后經過的A、B、C、D、E這幾個點點的坐標;
(2)按圖中所示規(guī)律,找到下一個點F的位置并寫出它的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,點E為矩形ABCD邊AD上一點,點P點Q同時從點B出發(fā),點P沿BE→ED→DC運動到點C停止,點Q沿BC運動到點C停止,它們的運動速度都是1cm/s.設P,Q出發(fā)t秒時,△BPQ的面積為y cm2,已知y與t的函數關系的圖象如圖2(曲線OM為拋物線的一部分).則下列結論:①AD=BE=5cm;②當0<t≤5時,![]() ;③直線NH的解析式為y=
;③直線NH的解析式為y=![]() t+27; ④若△ABE與△QBP相似,則t=
t+27; ④若△ABE與△QBP相似,則t=![]() 秒, 其中正確結論的個數為( )
秒, 其中正確結論的個數為( )


A. 1個B. 2個C. 3個D. 4個
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com