
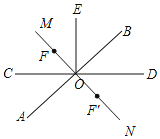
【題目】已知:如圖,直線AB、CD相交于點O,EO⊥CD于O.
(1)若∠AOC=36°,求∠BOE的度數;
(2)若∠BOD:∠BOC=1:5,求∠AOE的度數;
(3)在(2)的條件下,請你過點O畫直線MN⊥AB,并在直線MN上取一點F(點F與O不重合),然后直接寫出∠EOF的度數.

【答案】(1)54°;(2)120°;(3)∠EOF的度數為30°或150°.
【解析】
(1)依據垂線的定義以及對頂角相等,即可得∠BOE的度數;
(2)依據平角的定義以及垂線的定義,即可得到∠AOE的度數;
(3)分兩種情況:若F在射線OM上,則∠EOF=∠BOD=30°;若F'在射線ON上,則∠EOF'=∠DOE+∠BON-∠BOD=150°.
解:(1)∵EO⊥CD,
∴∠DOE=90°,
又∵∠BOD=∠AOC=36°,
∴∠BOE=90°-36°=54°;
(2)∵∠BOD:∠BOC=1:5,
∴∠BOD=![]() ∠COD=30°,
∠COD=30°,
∴∠AOC=30°,
又∵EO⊥CD,
∴∠COE=90°,
∴∠AOE=90°+30°=120°;
(3)分兩種情況:
若F在射線OM上,則∠EOF=∠BOD=30°;
若F'在射線ON上,則∠EOF'=∠DOE+∠BON-∠BOD=150°;
綜上所述,∠EOF的度數為30°或150°.
故答案為:(1)54°;(2)120°;(3)∠EOF的度數為30°或150°.


科目:初中數學 來源: 題型:
【題目】貴州省是我國首個大數據綜合試驗區,大數據在推動經濟發展、改善公共服務等方面日益顯示出巨大的價值,為創建大數據應用示范城市,我市某機構針對市民最關心的四類生活信息進行了民意調查(被調查者每人限選一項),下面是部分四類生活信息關注度統計圖表,請根據圖中提供的信息解答下列問題:

(1)本次參與調查的人數有 人;
(2)關注城市醫療信息的有 人,并補全條形統計圖;
(3)扇形統計圖中,D部分的圓心角是 度;
(4)說一條你從統計圖中獲取的信息.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖:在四邊形ABCD中,A、B、C、D四個點的坐標分別是:(-2,0)、(0,6)、(4,4)、(2,0)現將四邊形ABCD先向上平移1個單位,再向左平移2個單位,平移后的四邊形是A'B'C′D'
(1)請畫出平移后的四邊形A'B'C′D'(不寫畫法),并寫出A'、B'、C′、D'四點的坐標.
(2)若四邊形內部有一點P的坐標為(a,b)寫點P的對應點P′的坐標.
(3)求四邊形ABCD的面積.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】有規律排列的一列數:2,4,6,8,10,12,…,它的每一項可用式子2n(n是正整數)來表示.那么有規律排列的一列數:-1,2,-4,7,-11,16,-22,29,….
(1)它的第10個數是多少?
(2)你認為它的第n項可用怎樣的式子來表示?
(3)2018是不是這列數中的數?如果是,是第幾個數?如果不是,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在四邊形ABCD中,∠ABC=90°,AC=AD,M,N分別為AC,AD的中點,
且∠ABM=∠BAM,連接BM,MN,BN.
(1)求證:BM=MN;
(2)∠BAD=60°,AC平分∠BAD,AC=2,求BN的長.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】中學生騎電動車上學給交通安全帶來隱患,為了解某中學2 500個學生家長對“中學生騎電動車上學”的態度,從中隨機調查400個家長,結果有360個家長持反對態度,則下列說法正確的是( )
A. 調查方式是普查 B. 該校只有360個家長持反對態度
C. 樣本是360個家長 D. 該校約有90%的家長持反對態度
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】每年農歷五月初五,是中國民間的傳統節日——端午節.它始于我國的春秋戰國時期,已列為世界非物質文化遺產.時至今日,端午節在我國仍是一個十分盛行的節日.今年端午節,某地甲、乙兩家超市為吸引更多的顧客,開展促銷活動,對某種質量和售價相同的粽子分別推出了不同的優惠方案.甲超市的方案是:購買該種粽子超過80元后,超出80元的部分按九折收費;乙超市的方案是:購買該種粽子超過120元后,超出120元的部分按八折收費.請根據顧客購買粽子的金額,選擇到哪家超市購買粽子劃算?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在![]() 中,
中,![]() ,點
,點![]() 是直線
是直線![]() 上一點(不與
上一點(不與![]() 重合),以
重合),以![]() 為一邊在
為一邊在![]() 的右側作
的右側作![]() ,使
,使![]() ,
,![]() ,連接
,連接![]() .
.

(1)如圖1,當點![]() 在線段
在線段![]() 上時.如果
上時.如果![]() ,則
,則![]() __________.
__________.
(2)設![]() ,
,![]() .
.
①如圖2,當點![]() 在線段
在線段![]() 上移動時,
上移動時,![]() 之間有怎樣的數量關系?請說明理由.
之間有怎樣的數量關系?請說明理由.
②當點![]() 在直線
在直線![]() 上移動時,
上移動時,![]() 之間有怎樣的數量關系?請直接寫出你的結論.
之間有怎樣的數量關系?請直接寫出你的結論.
查看答案和解析>>
科目:初中數學 來源: 題型:
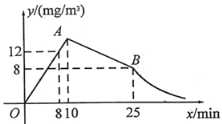
【題目】春季是流感高發的季節,為此,某校為預防流感,對教室進行熏藥消毒.在對教室進行消毒的過程中,先經過10min的藥物燃燒,再封閉教室15min,然后打開門窗進行通風.已知室內空氣中含藥量![]() 與藥物在空氣中的持續時間
與藥物在空氣中的持續時間![]() 之間的函數關系式如圖所示(即圖中線段OA、線段AB和雙曲線在點B及其右側部分),請根據圖中信息解答下列問題:
之間的函數關系式如圖所示(即圖中線段OA、線段AB和雙曲線在點B及其右側部分),請根據圖中信息解答下列問題:
(1)求藥物燃燒階段和打開門窗進行通風階段![]() 與
與![]() 之間的函數表達式;
之間的函數表達式;
(2)若室內空氣中的含藥量不低于![]() 且持續時間不少于35min,才能有效消滅病毒,則此次消毒是否有效?請說明理由.
且持續時間不少于35min,才能有效消滅病毒,則此次消毒是否有效?請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com