
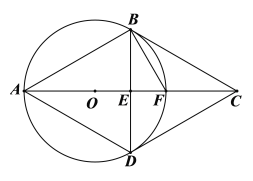
【題目】如圖,菱形ABCD對角線交于點E,△ABD的外接圓⊙O交AC于點F.若FB=FC.
(1)證明:![]() =FEFA;
=FEFA;
(2)證明:BC是⊙O的切線;
(3)若EF=2,求出四邊形ABCD的面積.
【答案】(1)見解析;(2)見解析;(3)![]()
【解析】
(1)首先根據菱形的性質和圓周角定理的推論得出△BEF∽△ABF,則有![]() ,即
,即![]() ,又因為FB=FC,則結論可證;
,又因為FB=FC,則結論可證;
(2)首先根據等腰三角形的性質和等量代換得出∠ABO=∠FBC,又因為∠ABO+∠FBO=∠ABF=90°,則有∠CBF+∠FBO =90°,進而可證明結論;
(3)首先根據三角形外角的性質和三角形內角和定理得出∠BAF=30°,∠BFA =60°,然后解直角三角形可求出AE,BE的長度,進而可求AC,BD的長度,最后利用菱形的面積公式即可求解.
(1)證明:∵四邊形ABCD是菱形,
∴AC垂直平分BD,
∵AF為⊙O的直徑.
∴∠ABF=90°.
![]() ,
,
∴△BEF∽△ABF.
∴![]() .
.
∴![]() .
.
∵FB=FC,
∴![]() =FEFA;
=FEFA;
(2)證明:連接OB,

∵OB=OA,FB=FC,BA=BC,
∴∠OBA=∠BAC,∠FBC=∠FCB,∠BAC=∠BCA.
∴∠ABO=∠FBC.
∵∠ABO+∠FBO=∠ABF=90°.
∴∠CBF+∠FBO =90°.
∴OB⊥BC.
∴BC是⊙O的切線;
(3)解:由(2)得∠BAC=∠BCA=∠FBC.
∴∠BFA=∠FBC+∠FCB=2∠FCB=2∠BAC.
∵∠BAF+∠BFA=180°-∠ABF=90°.
∴3∠BAF=90°.
∴∠BAF=30°.
∴∠BFA=2∠BAF=60°.
在Rt△BFE中,BE=EF![]() tan∠BFE=2
tan∠BFE=2![]() =
=![]() .
.
在Rt△BAE中,AE=![]() .
.
∴AC=2AE=12,BD=2BE=![]() .
.
∴四邊形ABCD的面積S=![]() .
.


 數學奧賽暑假天天練南京大學出版社系列答案
數學奧賽暑假天天練南京大學出版社系列答案 南大教輔搶先起跑暑假銜接教程南京大學出版社系列答案
南大教輔搶先起跑暑假銜接教程南京大學出版社系列答案科目:初中數學 來源: 題型:
【題目】如圖,矩形ABCD中,AB=3,BC=4,點E是A邊上一點,且AE=![]() ,點F是邊BC上的任意一點,把△BEF沿EF翻折,點B的對應點為G,連接AG,CG,則四邊形AGCD的面積的最小值為_____.
,點F是邊BC上的任意一點,把△BEF沿EF翻折,點B的對應點為G,連接AG,CG,則四邊形AGCD的面積的最小值為_____.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】中學生上學帶手機的現象越來越受到社會的關注,為此媒體記者隨機調查了某校若干名學生上學帶手機的目的,分為四種類型:A接聽電話;B收發短信;C查閱資料;D游戲聊天.并將調查結果繪制成圖1和圖2的統計圖(不完整),請根據圖中提供的信息,解答下列問題:
(1)此次抽樣調查中,共調查了 名學生;
(2)將圖1、圖2補充完整;
(3)現有4名學生,其中A類兩名,B類兩名,從中任選2名學生,求這兩名學生為同一類型的概率(用列表法或樹狀圖法).

查看答案和解析>>
科目:初中數學 來源: 題型:
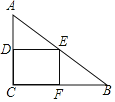
【題目】如圖,在RT△ABC中,∠ACB=90°,AC=6,BC=8,矩形CDEF的頂點E為AB的中點,D,F兩點分別在邊AC,BC上,且![]() ,將矩形CDEF以每秒1個單位長度的速度沿射線CB方向勻速運動,當點C與點B重合時停止運動,設運動時間為t秒,矩形CDEF與△ABC重疊部分的面積為S,則反映S與t的函數關系的圖象為( )
,將矩形CDEF以每秒1個單位長度的速度沿射線CB方向勻速運動,當點C與點B重合時停止運動,設運動時間為t秒,矩形CDEF與△ABC重疊部分的面積為S,則反映S與t的函數關系的圖象為( )
A.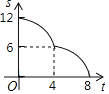 B.
B.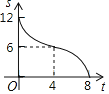
C.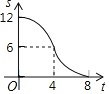 D.
D.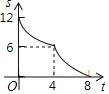
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某校計劃廠家購買A、B兩種型號的電腦,已知每臺A種型號電腦比每臺B種型號電腦多01.萬元,且用10萬元購買A種型號電腦的數量與用8萬元購買B種型號電腦的數量相同;
(1)求A、B兩種型號電腦單價各為多少萬元?
(2)學校預計用不多于9.2萬元的資金購進20臺電腦,其中A種型號電腦至少要購進10臺,請問有哪幾種購買方案?
查看答案和解析>>
科目:初中數學 來源: 題型:
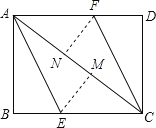
【題目】如圖,AC為矩形ABCD的對角線,將邊AB沿AE折疊,使點B落在AC上的點M處,將邊CD沿CF折疊,使點D落在AC上的點N處.
(1)求證:四邊形AECF是平行四邊形;
(2)當AB與AC滿足怎樣數量關系時,四邊形AECF為菱形.
查看答案和解析>>
科目:初中數學 來源: 題型:
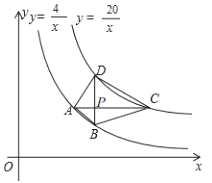
【題目】如圖,四邊形ABCD的四個頂點分別在反比例函數![]() 與
與![]() 的圖象上,對角線
的圖象上,對角線![]() 軸,且
軸,且![]() 于點P.已知點B的橫坐標為4.
于點P.已知點B的橫坐標為4.
(1)若點P的縱坐標為2,求直線AB的函數表達式.
(2)若點P是BD的中點,試判斷四邊形ABCD的形狀,并說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知銳角∠AOB如圖,(1)在射線OA上取一點C,以點O為圓心,OC長為半徑作![]() ,交射線OB于點D,連接CD;
,交射線OB于點D,連接CD;
(2)分別以點C,D為圓心,CD長為半徑作弧,交![]() 于點M,N;
于點M,N;
(3)連接OM,MN.
根據以上作圖過程及所作圖形,下列結論中錯誤的是( )

A. ∠COM=∠CODB. 若OM=MN,則∠AOB=20°
C. MN∥CDD. MN=3CD
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com