
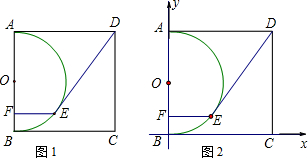
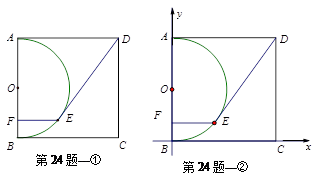
在邊長為10的正方形ABCD中,以AB為直徑作半圓O,如圖①,E是半圓上一動點,過點E作EF⊥AB,垂足為F,連結DE.
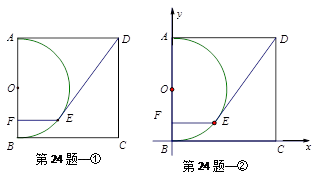
1.當DE=10時,求證:DE與圓O相切;
2.求DE的最長距離和最短距離;
3.如圖②,建立平面直角坐標系,當DE =10時,試求直線DE的解析式.
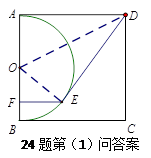
1.證明:連結![]() ,由題意得,------------1分
,由題意得,------------1分
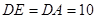 ,
,![]() ,
,![]() 為公共邊
為公共邊
∴![]()
![]()
∴![]() -------------------2分
-------------------2分
(利用勾股定理逆定理相應給分)
∴![]()
∴![]() 與圓
與圓![]() 相切.-------------------3分
相切.-------------------3分
2.當點![]() 運動到與
運動到與![]() 點重合的位置時,
點重合的位置時,
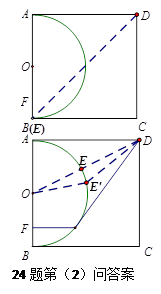
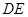 為正方形
為正方形![]() 的對角線,所以此時
的對角線,所以此時![]() 最長,有:
最長,有:
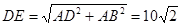 -----------------4分
-----------------4分
當點![]() 運動到線段
運動到線段![]() 與半圓
與半圓![]() 的交點處時,
的交點處時,![]() 最短.
最短.
-----------------5分
3.當點E與點A重合時,DE=DA=10,此時,直線DE的解析式為y=10;

當點E與點A不重合時,過點E作GH ⊥![]() 軸,分別交
軸,分別交![]() ,
,![]() 軸于點
軸于點![]() ,
,![]() ,連結
,連結![]() .
.
則四邊形![]() 是矩形,且
是矩形,且![]() 為圓
為圓![]() 的切線
的切線
∴![]() =90°
=90°
∴![]() -----------------------9分
-----------------------9分
又∵![]()
∴![]() ∽
∽![]()
∴![]() ----------------------10分
----------------------10分
設![]() ,則有:
,則有:![]() ,
,![]()
得:![]() ,-----------------------11分
,-----------------------11分
解得:![]() , 即:
, 即:![]() ----------------12分
----------------12分
又直線DE過點D(10,10),設直線![]() 解析式為
解析式為![]() ,則有:
,則有:![]() ,
,
解得: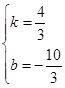 ,即:
,即:![]()
∴當![]() 時,直線
時,直線![]() 的解析式為
的解析式為![]() 或
或![]() -----------------------14分
-----------------------14分
以下兩種解法涉及高中知識,僅供參考:
另解2:
(1)當點E與點A重合時,DE=DA=10,此時,直線DE的解析式為y=10;
(2)當點E與點A不重合時,![]() ,
,
![]()
設直線![]() 且經過點(10,10),代入求得
且經過點(10,10),代入求得![]()
所以直線DE的解析式為![]()
另解3:
依題意得:點O的坐標為(0,5),設直線DE的解析式為![]()
由點到直線的距離公式得: ![]() ,即
,即![]() ①
①
直線DE過點D(10,10),得![]() ②
②
由①②解得:![]() ,解得
,解得![]()
所以直線DE的解析式為
解析:略


 培優好卷單元加期末卷系列答案
培優好卷單元加期末卷系列答案科目:初中數學 來源: 題型:
查看答案和解析>>
科目:初中數學 來源: 題型:
 定義:兩個直角三角形,若一個三角形的兩條直角邊分別與另一個三角形的兩條直角邊相等,我們就說這兩個直角三角形是“同胞直角三角形”.如圖,在邊長為10的正方形中有兩個直角三角形,當直角三角形①和直角三角形②是同胞直角三角形時,a的值是
定義:兩個直角三角形,若一個三角形的兩條直角邊分別與另一個三角形的兩條直角邊相等,我們就說這兩個直角三角形是“同胞直角三角形”.如圖,在邊長為10的正方形中有兩個直角三角形,當直角三角形①和直角三角形②是同胞直角三角形時,a的值是查看答案和解析>>
科目:初中數學 來源: 題型:
查看答案和解析>>
科目:初中數學 來源:2011-2012學年廣東省九年級下學期第一次模擬數學卷(解析版) 題型:解答題
在邊長為10的正方形ABCD中,以AB為直徑作半圓O,如圖①,E是半圓上一動點,過點E作EF⊥AB,垂足為F,連結DE.
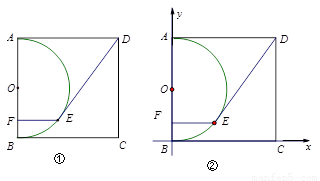
(1)當DE=10時,求證:DE與圓O相切;
(2)求DE的最長距離和最短距離;
(3)如圖②,建立平面直角坐標系,當DE =10時,試求直線DE的解析式.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com