
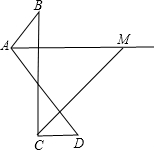
 已知如圖,∠B=32°,∠D=38°,AM、CM分別平分∠BAD和∠BCD.
已知如圖,∠B=32°,∠D=38°,AM、CM分別平分∠BAD和∠BCD.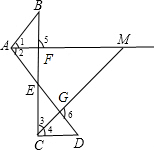 解:(1)如圖,∵AM、CM分別平分∠BAD和∠BCD,
解:(1)如圖,∵AM、CM分別平分∠BAD和∠BCD, =(∠B+
=(∠B+ ,
, =(∠B+∠D)×
=(∠B+∠D)× ,
, (∠B+∠D).
(∠B+∠D). (∠B+∠D).
(∠B+∠D).

 教材全解字詞句篇系列答案
教材全解字詞句篇系列答案科目:初中數學 來源: 題型:
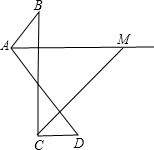 已知如圖,∠B=32°,∠D=38°,AM、CM分別平分∠BAD和∠BCD.
已知如圖,∠B=32°,∠D=38°,AM、CM分別平分∠BAD和∠BCD.查看答案和解析>>
科目:初中數學 來源:1998年河北省中考數學試卷(解析版) 題型:選擇題
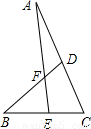
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com