
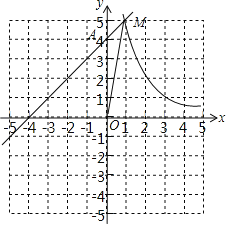
【題目】在平面直角坐標系xOy中,一次函數y=x+4的圖象與y軸交于點A,與反比例函數y=![]() 的圖象的一個交點為M.
的圖象的一個交點為M.
(1)求點A的坐標;
(2)連接OM,如果△MOA的面積等于2,求k的值.
【答案】(1)A(0,4);(2)5或﹣3
【解析】
(1)通過計算自變量為0對應的一次函數值得到A點坐標;
(2)利用一次函數圖象上點的坐標特征,設M點的坐標為(t,t+4),根據三角形面積公式得到![]() ×4×|t|=2,求出t得到M點的坐標,然后利用反比例函數圖象上點的坐標特征求k的值.
×4×|t|=2,求出t得到M點的坐標,然后利用反比例函數圖象上點的坐標特征求k的值.
解:(1)當x=0,y=x+4=4,
∴A(0,4);
(2)設M點的坐標為(t,t+4),
∵△MOA的面積等于2,
∴![]() ×4×|t|=2,解得t=1或t=﹣1,
×4×|t|=2,解得t=1或t=﹣1,
∴M點的坐標為(1,5)或(﹣1,3),
當M點的坐標為(1,5)時,k=1×5=5;
當M點的坐標為(﹣1,3)時,k=﹣1×3=﹣3,
綜上所述,k的值為5或﹣3.


科目:初中數學 來源: 題型:
【題目】在平面直角坐標系xOy中,直線x=3與直線y=![]() x+1交于點A,函數y=
x+1交于點A,函數y=![]() (k>0,x>0)的圖象與直線x=3,直線y=
(k>0,x>0)的圖象與直線x=3,直線y=![]() x+1分別交于點B,C.
x+1分別交于點B,C.
(1)求點A的坐標.
(2)橫、縱坐標都是整數的點叫做整點.記函數y=![]() (k>0,x>0)的圖象在點B,C之間的部分與線段AB,AC圍成的區域(不含邊界)為W.
(k>0,x>0)的圖象在點B,C之間的部分與線段AB,AC圍成的區域(不含邊界)為W.
①當k=1時,結合函數圖象,求區域W內整點的個數;
②若區域W內恰有1個整點,直接寫出k的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在平面直角坐標系xOy中,拋物線y=mx2﹣6mx+9m+1(m≠0).
(1)求拋物線的頂點坐標;
(2)若拋物線與x軸的兩個交點分別為A和B點(點A在點B的左側),且AB=4,求m的值.
(3)已知四個點C(2,2)、D(2,0)、E(5,﹣2)、F(5,6),若拋物線與線段CD和線段EF都沒有公共點,請直接寫出m的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】ABCD中,對角線AC、BD相交于點O,E是邊AB上的一個動點(不與A、B重合),連接EO并延長,交CD于點F,連接AF,CE,下列四個結論中:
①對于動點E,四邊形AECF始終是平行四邊形;
②若∠ABC<90°,則至少存在一個點E,使得四邊形AECF是矩形;
③若AB>AD,則至少存在一個點E,使得四邊形AECF是菱形;
④若∠BAC=45°,則至少存在一個點E,使得四邊形AECF是正方形.
以上所有正確說法的序號是_____.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在平面直角坐標系xOy中,已知拋物線y=ax2+bx﹣1交y軸于點P.
(1)過點P作與x軸平行的直線,交拋物線于點Q,PQ=4,求![]() 的值;
的值;
(2)橫縱坐標都是整數的點叫做整點.在(1)的條件下,記拋物線與x軸所圍成的封閉區域(不含邊界)為W.若區域W內恰有4個整點,結合函數圖象,求a的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知二次函數y=ax2﹣2ax.
(1)二次函數圖象的對稱軸是直線x= ;
(2)當0≤x≤3時,y的最大值與最小值的差為4,求該二次函數的表達式;
(3)若a<0,對于二次函數圖象上的兩點P(x1,y1),Q(x2,y2),當t≤x1≤t+1,x2≥3時,均滿足y1≥y2,請結合函數圖象,直接寫出t的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】先進制造業城市發展指數是反映一個城市先進制造水平的綜合指數.對2019年我國先進制造業城市發展指數得分排名位居前列的30個城市的有關數據進行收集、整理、描述和分析.下面給出了部分信息:
a.先進制造業城市發展指數得分的頻數分布直方圖(數據分成6組:![]() ):
):
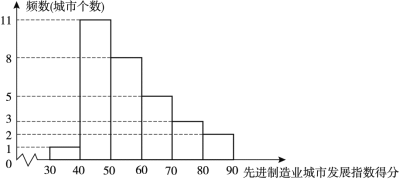
b.先進制造業城市發展指數得分在![]() 這一組的是:71.1 75.7 79.9
這一組的是:71.1 75.7 79.9
c.30個城市的2019年快遞業務量累計和先進制造業城市發展指數得分情況統計圖:
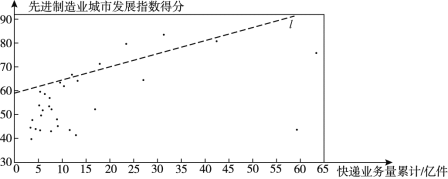
d.北京的先進制造業城市發展指數得分為79.9.
根據以上信息,回答下列問題:
(1)在這30個城市中,北京的先進制造業城市發展指數排名第![]() ;
;
(2)在30個城市的快遞業務量累計和先進制造業城市發展指數得分情況統計圖中,包括北京在內的少數幾個城市所對應的點位于虛線![]() 的上方.請在圖中用“○”圈出代表北京的點;
的上方.請在圖中用“○”圈出代表北京的點;
(3)在這30個城市中,先進制造業城市發展指數得分高于北京的城市的快遞業務量累計的最小值約為_______億件.(結果保留整數)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,△ABC中,A,B兩個頂點在x軸上方,點C的坐標是(﹣1,0),以點C為位似中心,在x軸的下方作△ABC的位似圖形,并把△ABC的邊長放大到原來的2倍,得到△A'B'C',設點B的對應點B'的橫坐標為2,則點B的橫坐標為( )
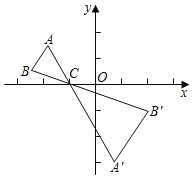
A.﹣1B.![]() C.﹣2D.
C.﹣2D.![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
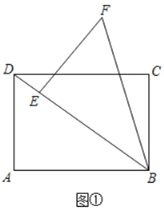
【題目】(操作)BD是矩形ABCD的對角線,AB=4,BC=3.將△BAD繞著點B順時針旋轉α度(0°<α<360°)得到△BEF,點A、D的對應點分別為E、F.若點E落在BD上,如圖①,則DE=______.
(探究)當點E落在線段DF上時,CD與BE交于點G.其它條件不變,如圖②.
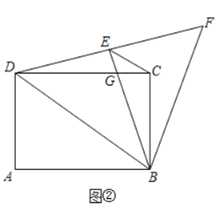
(1)求證:△ADB≌△EDB;
(2)CG的長為______.
(拓展)連結CF,在△BAD的旋轉過程中,設△CEF的面積為S,直接寫出S的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com