
【題目】如圖1,![]() 為半圓
為半圓![]() 的直徑,
的直徑,![]() 為
為![]() 的延長線上一點,
的延長線上一點,![]() 為半圓
為半圓![]() 的切線,切點為
的切線,切點為![]() .
.

(1)求證:![]() ;
;
(2)如圖2,![]() 的平分線分別交
的平分線分別交![]() ,
,![]() 于點
于點![]() ,
,![]() .
.
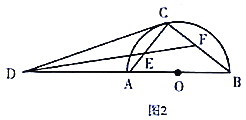
①求![]() 的值;
的值;
②若![]() ,
,![]() ,求
,求![]() 的長.
的長.
 名校課堂系列答案
名校課堂系列答案科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,⊙O的直徑為AB,點C在圓周上(異于A,B),AD⊥CD.
(1)若BC=3,AB=5,求AC的值;
(2)若AC是∠DAB的平分線,求證:直線CD是⊙O的切線.

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】農(nóng)經(jīng)公司以30元/千克的價格收購一批農(nóng)產(chǎn)品進(jìn)行銷售,為了得到日銷售量p(千克)與銷售價格x(元/千克)之間的關(guān)系,經(jīng)過市場調(diào)查獲得部分?jǐn)?shù)據(jù)如下表:
銷售價格x(元/千克) | 30 | 35 | 40 | 45 | 50 |
日銷售量p(千克) | 600 | 450 | 300 | 150 | 0 |
(![]() )請你根據(jù)表中的數(shù)據(jù),寫出一個符合p與x的函數(shù)表達(dá)式__________.
)請你根據(jù)表中的數(shù)據(jù),寫出一個符合p與x的函數(shù)表達(dá)式__________.
(![]() )農(nóng)經(jīng)公司應(yīng)該如何確定這批農(nóng)產(chǎn)品的銷售價格,才能使日銷售利潤最大?
)農(nóng)經(jīng)公司應(yīng)該如何確定這批農(nóng)產(chǎn)品的銷售價格,才能使日銷售利潤最大?
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,在平面直角坐標(biāo)系![]() 中有矩形
中有矩形![]() ,
,![]() ,將矩形
,將矩形![]() 繞原點
繞原點![]() 逆時針旋轉(zhuǎn)得到矩形OA′B′C′.
逆時針旋轉(zhuǎn)得到矩形OA′B′C′.
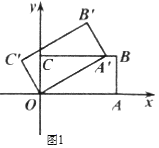
(Ⅰ)如圖1,當(dāng)點A′首次落在![]() 上時,求旋轉(zhuǎn)角;
上時,求旋轉(zhuǎn)角;
(Ⅱ)在(Ⅰ)的條件下求點B′的坐標(biāo);
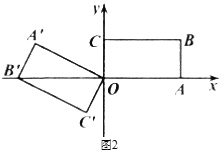
(Ⅲ)如圖2,當(dāng)點B′首次落在![]() 軸上時,直接寫出此時點A′的坐標(biāo).
軸上時,直接寫出此時點A′的坐標(biāo).
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
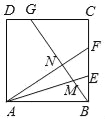
【題目】如圖,正方形ABCD中,BE=EF=FC,CG=2GD,BG分別交AE,AF于M,N.下列結(jié)論:①AF⊥BG;②BN=![]() NF;③
NF;③![]() ;④S四邊形CGNF=
;④S四邊形CGNF=![]() S四邊形ANGD.其中正確的結(jié)論的序號是 .
S四邊形ANGD.其中正確的結(jié)論的序號是 .
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】已知二次函數(shù)y=﹣x2﹣2x+3.
(1)把函數(shù)關(guān)系式配成頂點式并求出圖象的頂點坐標(biāo)和對稱軸.
(2)若圖象與x軸交點為A.B,與y軸交點為C,求A、B、C三點的坐標(biāo);
(3)在圖中畫出圖象.并求出△ABC面積.

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖(1),已知∠![]() ,點
,點![]() 為射線
為射線![]() 上一點,且
上一點,且![]() ,
,![]() 、
、![]() 為射線
為射線![]() 和
和![]() 上的兩個動點(
上的兩個動點(![]() ),過點
),過點![]() 作
作![]() ⊥
⊥![]() ,垂足為點
,垂足為點![]() ,且
,且![]() ,聯(lián)結(jié)
,聯(lián)結(jié)![]() .
.
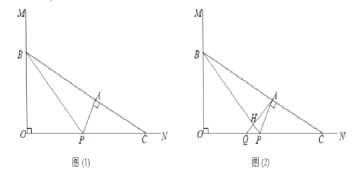
(1)若![]() 時,求
時,求![]() 的值;
的值;
(2)設(shè)![]() ,
,![]() 求
求![]() 與
與![]() 之間的函數(shù)解析式,并寫出定義域;
之間的函數(shù)解析式,并寫出定義域;
(3)如圖(2),過點![]() 作
作![]() 的垂線,垂足為點
的垂線,垂足為點![]() ,交射線
,交射線![]() 于點
于點![]() ,點
,點![]() 、
、![]() 在射線
在射線![]() 和
和![]() 上運動時,探索線段
上運動時,探索線段![]() 的長是否發(fā)生變化?若不發(fā)生變化,求出它的值。若發(fā)生變化,試用含x的代數(shù)式表示
的長是否發(fā)生變化?若不發(fā)生變化,求出它的值。若發(fā)生變化,試用含x的代數(shù)式表示![]() 的長.
的長.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】閱讀下列材料,完成任務(wù):
自相似圖形
定義:若某個圖形可分割為若干個都與它相似的圖形,則稱這個圖形是自相似圖形.例如:
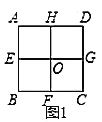
正方形![]() 中,點
中,點![]() 、
、![]() 、
、![]() 、
、![]() 分別是
分別是![]() 、
、![]() 、
、![]() 、
、![]() 邊的中點,連接
邊的中點,連接![]() ,
,![]() 交于點
交于點![]() ,易知分割成的四個四邊形
,易知分割成的四個四邊形![]() 、
、![]() 、
、![]() 、
、![]() 均為正方形,且與原正方形相似,故正方形是自相似圖形.
均為正方形,且與原正方形相似,故正方形是自相似圖形.
任務(wù):
(1)圖1中正方形![]() 分割成的四個小正方形中,每個正方形與原正方形的相似比為_______;
分割成的四個小正方形中,每個正方形與原正方形的相似比為_______;
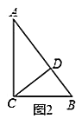
(2)如圖2,已知![]() 中,
中,![]() ,
,![]() ,
,![]() ,小明發(fā)現(xiàn)
,小明發(fā)現(xiàn)![]() 也是“自相似圖形”,他的思路是:過點
也是“自相似圖形”,他的思路是:過點![]() 作
作![]() 于點
于點![]() ,則
,則![]() 將
將![]() 分割成2個與它自己相似的小直角三角形.則
分割成2個與它自己相似的小直角三角形.則![]() 與
與![]() 的相似比為________;則
的相似比為________;則![]() 與
與![]() 的相似比為_______;
的相似比為_______;
(3)現(xiàn)有一個矩形![]() 是自相似圖形,其中長
是自相似圖形,其中長![]() ,寬
,寬![]() .
.
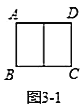
①如圖3-1,若將矩形![]() 縱向分割成兩個全等矩形,且與原矩形都相似,則
縱向分割成兩個全等矩形,且與原矩形都相似,則![]() _____(用含
_____(用含![]() 的式子表示);
的式子表示);
②如圖3-2若將矩形![]() 縱向分割成
縱向分割成![]() 個全等矩形,且與原矩形都相似,則
個全等矩形,且與原矩形都相似,則![]() ______(用含
______(用含![]() ,
,![]() 的式子表示);
的式子表示);

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】已知一次函數(shù)y=-![]() x+6的圖象與坐標(biāo)軸交于A、B點(如圖),AE平分∠BAO,交x軸于點E.
x+6的圖象與坐標(biāo)軸交于A、B點(如圖),AE平分∠BAO,交x軸于點E.

(1)求點B的坐標(biāo);
(2)求直線AE的表達(dá)式;
(3)過點B作BF⊥AE,垂足為F,連接OF,試判斷△OFB的形狀,并求△OFB的面積.
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com