
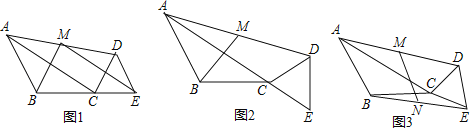
【題目】在△ABC中,AB=BC=2![]() ,∠ABC=120°,△CDE為等邊三角形,CD=2,連接AD,M為AD中點.
,∠ABC=120°,△CDE為等邊三角形,CD=2,連接AD,M為AD中點.
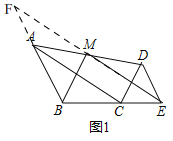
(1)如圖1,當B,C,E三點共線時,請畫出△EDM關于點M的中心對稱圖形,并證明BM⊥ME;
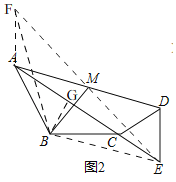
(2)如圖2,當A,C,E三點共線時,求BM的長;
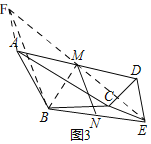
(3)如圖3,取BE中點N,連MN,將△CDE繞點C旋轉,直接寫出旋轉過程中線段MN的取值范圍是_____.
【答案】(1)答案見解析;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)先作出圖形,進而證明△AMF≌△DME,即可得出結論;
(2)同(1)的方法得出△AMF≌△DMF,利用四邊形的內角和定理及平角的定義得出∠BCE=∠BAF即可得出∠BME=90°,最后用勾股定理即可得出結論;
(3)同(2)的方法得出∠BME=90°,進而得出BE=2MN,最后用三角形的三邊關系即可得出結論.
解:(1)證明:如圖1,
延長BA,EM交于點F,即:△FAM即為所求,
∵△CDE是等邊三角形,
∴CD=CE=DE,∠CED=60°,
∵∠ABC=120°,
∴∠ABC+∠CED=180°,
∵B,C,E三點共線,
∴AB∥DE,
∴∠FAM=∠MDE,∠MED=∠F,
∵點M是AD中點,
∴AM=DM,
∴△AMF≌△DME,
∴AF=DE=CE,FM=ME,
∵AB=BC,
∴BF=BE,
∴BM⊥ME;
(2)證明:如圖2,延長EM到點F,使MF=ME,連接BF,AF,BE,
∵AM=DM,∠FMA=∠DME,
∴△AMF≌△DMF,
∴AF=DE=CE,∠FAD=∠ADE,
在四邊形BADE中,∵∠BAD+∠ADE+∠DEB+∠EBA=360°,
∵∠ABC=120°,∠CED=60°,
∴∠CBE+∠CEB+∠BAD+∠ADE=180°,
∵∠CBE+∠CEB+∠BCE=180°,
∴∠BCE=∠BAD+∠ADE,
∴∠BCE=∠BAF,
∵AB=AC,
∴△AFB≌△CEB,
∴BF=BE,∠ABF=∠CBE,
∴∠FBE=∠ABC=120°,∠BEF=30°,
∴∠BME=90°,BE=2BM.
在△ABC中,AB=AC=2![]() ,∠ABC=120°,∴∠BAC=30°,
,∠ABC=120°,∴∠BAC=30°,
過點B作BG⊥AC于G,
∴BG=![]() ,CG=AG=3,
,CG=AG=3,
∴EG=CG+CE=3+2=5
在Rt△BCE中,根據勾股定理得,BE=2![]() ,
,
∴BM=![]() ;
;
(3)如圖3,延長EM到點F,使MF=ME,連接BF,AF,BM,
∵AM=DM,∠FMA=∠DME,
∴△AMF≌△DME,
∴AF=DE=CE,∠FAD=∠ADE,
在四邊形BADE中,∵∠BAD+∠ADE+∠DEB+∠EBA=360°,
∵∠ABC=120°,∠CED=60°,
∴∠CBE+∠CEB+∠BAD+∠ADE=180°,
∵∠CBE+∠CEB+∠BCE=180°,
∴∠BCE=∠BAD+∠ADE,
∴∠BCE=∠BAF,
∵AB=CB,
∴△AFB≌△CEB,
∴BF=BE,∠ABF=∠CBE,
∴∠FBE=∠ABC=120°,∠BEF=30°,
∴∠BME=90°,
∵點N是BE的中點,
∴MN=![]() BE,
BE,
即:BE=2MN,
在△BCE中,BC=2![]() ,CE=CD=2,
,CE=CD=2,
∴2![]() ﹣2<BE<2
﹣2<BE<2![]() +2,
+2,
∴2![]() ﹣2<2MN<2
﹣2<2MN<2![]() +2,
+2,
即:![]() ﹣1≤MN≤
﹣1≤MN≤![]() +1,
+1,
故答案為:![]() ﹣1≤MN≤
﹣1≤MN≤![]() +1.
+1.


科目:初中數學 來源: 題型:
【題目】已知等邊△ABC,點D為BC上一點,連接AD.
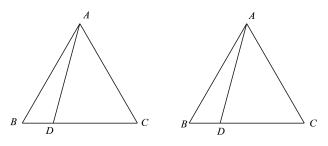
圖1 圖2
(1)若點E是AC上一點,且CE=BD,連接BE,BE與AD的交點為點P,在圖(1)中根據題意補全圖形,直接寫出∠APE的大小;
(2)將AD繞點A逆時針旋轉120°,得到AF,連接BF交AC于點Q,在圖(2)中根據題意補全圖形,用等式表示線段AQ和CD的數量關系,并證明.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某車庫出口安裝的欄桿如圖所示,點A是欄桿轉動的支點,點E是欄桿兩段的聯結點.當車輛經過時,欄桿AEF最多只能升起到如圖2所示的位置,其示意圖如圖3所示(欄桿寬度忽略不計),其中AB⊥BC,EF∥BC,∠AEF=143°,AB=1.18米,AE=1.2米,那么適合該地下車庫的車輛限高標志牌為( )(參考數據:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
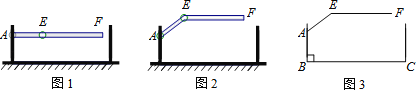
A. B.
B. C.
C. D.
D.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在我校舉辦的“讀好書、講禮儀”活動中,各班積極行動,圖書角的新書、好書不斷增多,除學校購買的圖書外,還有師生捐獻的圖書,下面是九(1)班全體同學捐獻圖書情況的統計圖(每人都有捐書).
請你根據以上統計圖中的信息,解答下列問題:
(1)該班有學生多少人?
(2)補全條形統計圖.
(3)九(1)班全體同學所捐圖書是 6 本的人數在扇形統計圖中所對應扇形的圓心角為多少度?
(4)請你估計全校 2000 名學生所捐圖書的數量.

查看答案和解析>>
科目:初中數學 來源: 題型:
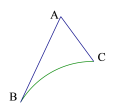
【題目】如圖所示,AB=6,AC=3,∠BAC=60°,![]() 為⊙O上的一段弧,且∠BOC=60°,分別在
為⊙O上的一段弧,且∠BOC=60°,分別在![]() 、線段AB和AC上選取點P、E、F,則PE+EF+FP的最小值為__________
、線段AB和AC上選取點P、E、F,則PE+EF+FP的最小值為__________
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某商品的進價為每件10元,現在的售價為每件15元,每周可賣出100件,市場調查反映:如果每件的售價每漲1元(售價每件不能高于20元),那么每周少賣10件.設每件漲價![]() 元(
元(![]() 為非負整數),每周的銷量為
為非負整數),每周的銷量為![]() 件.
件.
(1)求![]() 與
與![]() 的函數關系式及自變量
的函數關系式及自變量![]() 的取值范圍;
的取值范圍;
(2)如果經營該商品每周的利潤是560元,求每件商品的售價是多少元?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】閱讀下列材料,并完成相應的任務.
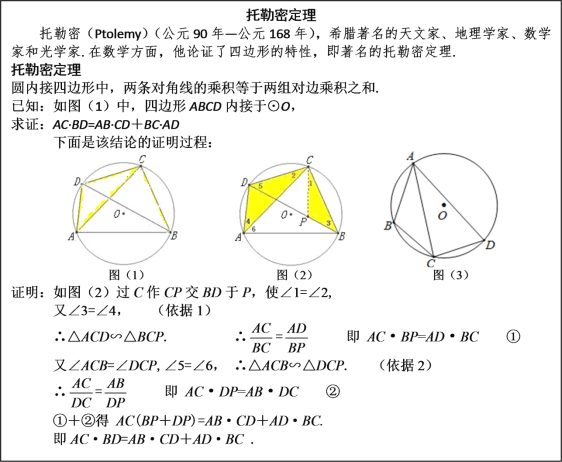
任務:
(1)上述證明過程中的“依據1”和“依據2”分別指什么?
依據1:
依據2:
(2)當圓內接四邊形ABCD是矩形時,托勒密定理就是我們非常熟知的一個定理: (請寫出定理名稱).
(3)如圖(3),四邊形ABCD內接于⊙O,AB=3,AD=5,∠BAD=60°,點C是弧BD的中點,求AC的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某新建火車站站前廣場需要綠化的面積為46000米2,施工隊在綠化了22000米2后,將每天的工作量增加為原來的1.5倍,結果提前4天完成了該項綠化工程.
(1)該項綠化工程原計劃每天完成多少米2?
(2)該項綠化工程中有一塊長為20米,寬為8米的矩形空地,計劃在其中修建兩塊相同的矩形綠地,它們的面積之和為56米2,兩塊綠地之間及周邊留有寬度相等的人行通道(如圖所示),問人行通道的寬度是多少米?

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知銳角∠AOB如圖,(1)在射線OA上取一點C,以點O為圓心,OC長為半徑作![]() ,交射線OB于點D,連接CD;
,交射線OB于點D,連接CD;
(2)分別以點C,D為圓心,CD長為半徑作弧,交![]() 于點M,N;
于點M,N;
(3)連接OM,MN.
根據以上作圖過程及所作圖形,下列結論中錯誤的是( )

A. ∠COM=∠CODB. 若OM=MN,則∠AOB=20°
C. MN∥CDD. MN=3CD
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com