
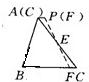
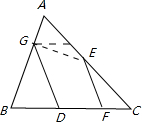
 23、在△ABC中,借助作圖工具可以作出中位線EF,沿著中位線EF一刀剪切后,用得到的△AEF和四邊形EBCF可以拼接成平行四邊形EBCP,剪切線與拼圖過程如圖所示,依照上述方法,按要求完成下列操作設計,并畫出圖形說明.
23、在△ABC中,借助作圖工具可以作出中位線EF,沿著中位線EF一刀剪切后,用得到的△AEF和四邊形EBCF可以拼接成平行四邊形EBCP,剪切線與拼圖過程如圖所示,依照上述方法,按要求完成下列操作設計,并畫出圖形說明.



 靈星計算小達人系列答案
靈星計算小達人系列答案 孟建平錯題本系列答案
孟建平錯題本系列答案科目:初中數學 來源: 題型:

查看答案和解析>>
科目:初中數學 來源: 題型:
查看答案和解析>>
科目:初中數學 來源: 題型:
| 1 | 2 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
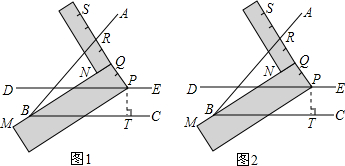 (1)閱讀理解:
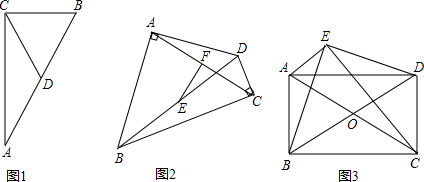
(1)閱讀理解: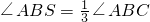 是否成立?如果成立,請說明理由;如果不成立,請在圖2中∠ABC的外部畫出
是否成立?如果成立,請說明理由;如果不成立,請在圖2中∠ABC的外部畫出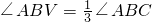 (無需寫畫法,保留畫圖痕跡即可).
(無需寫畫法,保留畫圖痕跡即可).查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com