
【題目】如圖,在Rt△ABC中,∠ACB=90°,∠B=60°,BC=2,△A′B′C可以由△ABC繞點C順時針旋轉得到,其中點A′與點A是對應點,點B′與點B是對應點,連接AB′,且A、B′、A′在同一條直線上,則AA′的長為( )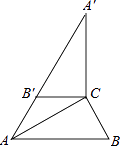
A.6
B.4 ![]()
C.3 ![]()
D.3
【答案】A
【解析】解:∵在Rt△ABC中,∠ACB=90°,∠B=60°,BC=2,
∴∠CAB=30°,故AB=4,
∵△A′B′C由△ABC繞點C順時針旋轉得到,其中點A′與點A是對應點,點B′與點B是對應點,連接AB′,且A、B′、A′在同一條直線上,
∴AB=A′B′=4,AC=A′C,
∴∠CAA′=∠A′=30°,
∴∠ACB′=∠B′AC=30°,
∴AB′=B′C=2,
∴AA′=2+4=6.
故答案為:A.
根據含30![]() 角的直角三角形的邊角關系得出AB的長,由旋轉的性質得AB=A′B′=4,AC=A′C,根據等邊對等角得出∠CAA′=∠A′=30°,進而得出∠ACB′=∠B′AC=30°,,根據等角對等邊得出AB′=B′C=2,,從而得出AA的長。
角的直角三角形的邊角關系得出AB的長,由旋轉的性質得AB=A′B′=4,AC=A′C,根據等邊對等角得出∠CAA′=∠A′=30°,進而得出∠ACB′=∠B′AC=30°,,根據等角對等邊得出AB′=B′C=2,,從而得出AA的長。


 新課標階梯閱讀訓練系列答案
新課標階梯閱讀訓練系列答案 口算心算速算應用題系列答案
口算心算速算應用題系列答案科目:初中數學 來源: 題型:
【題目】某開發公司生產的 960 件新產品需要精加工后,才能投放市場,現甲、乙兩個工廠都想加工這批產品,已知甲工廠單獨加工完成這批產品比乙工廠單獨加工完成這批產品多用 20 天,而甲工廠每天加工的數量是乙工廠每天加工的數量的![]() ,公司需付甲工廠加工費用為每天 80 元,乙工廠加工費用為每天 120 元.
,公司需付甲工廠加工費用為每天 80 元,乙工廠加工費用為每天 120 元.
(1)甲、乙兩個工廠每天各能加工多少件新產品?
(2)公司制定產品加工方案如下:可以由每個廠家單獨完成,也可以由兩個廠家合作完成.在加工過程中,公司派一名工程師每天到廠進行技術指導,并負擔每天 15 元的午餐補助費, 請你幫公司選擇一種既省時又省錢的加工方案,并說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】閱讀材料:
我們經常通過認識一個事物的局部或其特殊類型,來逐步認識這個事物;比如我們通過學習特殊的四邊形,即平行四邊形(繼續學習它們的特殊類型如矩形、菱形等)來逐步認識四邊形;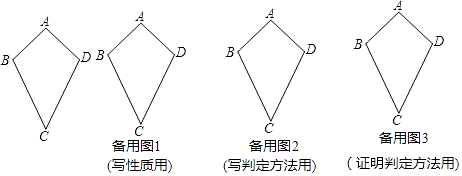
我們對課本里特殊四邊形的學習,一般先學習圖形的定義,再探索發現其性質和判定方法,然后通過解決簡單的問題鞏固所學知識;
請解決以下問題:
如圖,我們把滿足AB=AD、CB=CD且AB≠BC的四邊形ABCD叫做“箏形”;
(1)寫出箏形的兩個性質(定義除外);
(2)寫出箏形的兩個判定方法(定義除外),并選出一個進行證明.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】2015年4月份的尼泊爾強震曾經導致珠峰雪崩,在珠峰搶險時,需8組登山隊員步行運送物資,要求每組分配的人數相同,若按每組人數比預定人數多分配1人,則總數會超過100人;若按每組人數比預定人數少分配1人,則總數不夠90人,那么預定每組分配的人數是( )
A. 10 B. 11 C. 12 D. 13
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在平面直角坐標系xOy中, A、B兩點分別在x軸、y軸的正半軸上,且OB = OA=3.(1)、求點A、B的坐標;(2)、已知點C(-2,2),求△BOC的面積;(3)、點P是第一象限角平分線上一點,若![]() ,求點P的坐標.
,求點P的坐標.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在![]() 中,
中,![]() ,在
,在![]() 的外部作等邊三角形
的外部作等邊三角形![]() ,
,![]() 為
為![]() 的中點,連接
的中點,連接![]() 并延長交
并延長交![]() 于點
于點![]() ,連接
,連接![]() .
.
(1)如圖1,若![]() ,求
,求![]() 的度數;
的度數;
(2)如圖2,![]() 的平分線交
的平分線交![]() 于點
于點![]() ,交
,交![]() 于點
于點![]() ,連接
,連接![]() .
.
①補全圖2;
②若![]() ,求證:
,求證:![]() .
.

查看答案和解析>>
科目:初中數學 來源: 題型:
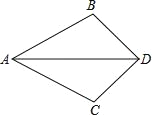
【題目】如圖,已知AD平分∠BAC,要使△ABD≌△ACD,
(1)根據“SAS”需添加條件________;
(2)根據“ASA”需添加條件________;
(3)根據“AAS”需添加條件________.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com