
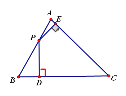
【題目】如圖,在△ABC中,∠C=45°,∠B=60°,BC為![]() +1,點P為邊AB上一動點,過點P作PD⊥BC于點D,PE⊥AC于點E,則DE的最小值為_____.
+1,點P為邊AB上一動點,過點P作PD⊥BC于點D,PE⊥AC于點E,則DE的最小值為_____.
【答案】![]()
【解析】
當CP⊥AB時,線段DE的值最小,利用四點共圓的判定可得:C、D、P、E四點共圓,且直徑為CP,由∠B=60°,BC為![]() +1,求出PC,從而得出半徑OD的長度,然后由∠ACB=45°,得到∠EOD=90°,利用等腰直角三角形的性質,可求出DE的值.
+1,求出PC,從而得出半徑OD的長度,然后由∠ACB=45°,得到∠EOD=90°,利用等腰直角三角形的性質,可求出DE的值.
解:當CP⊥AB時,線段DE的值最小(因為四邊形C、D、P、E四點共圓,PC是直徑,BC=![]() 和∠B=60°是定值,所以直徑CP最小時,∠DCE所對的弦DE最小);如圖:
和∠B=60°是定值,所以直徑CP最小時,∠DCE所對的弦DE最小);如圖:

∵PD⊥BC于D,PE⊥AC于E,
∴∠CDP=∠AEP=90°,
∴∠CDP+∠AEP=180°,
∴C、D、P、E四點共圓,且直徑為CP,
∵∠B=60°,CP⊥AB,BC=![]() ,
,
∴![]() ,即
,即![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵∠ACB=45°,
∴∠EOD=90°,
∴△OED是等腰直角三角形,
∴![]() ;
;
∴DE的最小值為:![]() .
.
故答案為:![]() .
.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
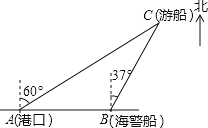
【題目】 一艘觀光游船從港口A以北偏東60°的方向出港觀光,航行80海里至C處時發生了側翻沉船事故,立即發出了求救信號,一艘在港口正東方向的海警船接到求救信號,測得事故船在它的北偏東37°方向,馬上以40海里每小時的速度前往救援,求海警船到大事故船C處所需的大約時間.(溫馨提示:sin53°≈0.8,cos53°≈0.6)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知![]() 是
是![]() 的直徑,
的直徑,![]() 是
是![]() 的弦,
的弦,![]() 平分
平分![]() 交
交![]() 于點
于點![]() ,連接
,連接![]() 、
、![]() ,過點
,過點![]() 作
作![]() ,交
,交![]() 的延長線于點
的延長線于點![]() .
.
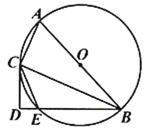
(1)![]() ________
________![]() (填“>”,“<”或“=”);
(填“>”,“<”或“=”);
(2)求證:![]() 是
是![]() 的切線;
的切線;
(3)若![]() 的直徑為10,sin∠BAC=
的直徑為10,sin∠BAC=![]() ,求
,求![]() 的長.
的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
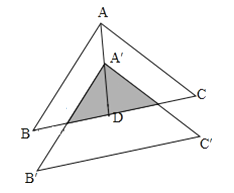
【題目】如圖,將△ABC沿BC邊上的中線AD平移到△A′B′C′的位置,已知△ABC的面積為18,陰影部分三角形的面積為8,若AA′=1,則A′D的值為______.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】定義:我們把關于某一點成中心對稱的兩條拋物線叫“孿生拋物線”;(1)已知拋物線L:y=﹣x2+4與x軸交于A、B兩點(A在B的左側),與y軸交于C點,求L關于坐標原點O(0,0)的“孿生拋物線”W;(2)點N為坐標平面內一點,且△BCN是以BC為斜邊的等腰直角三角形,在x軸是否存在一點M(m,0),使拋物線L關于點M的“孿生拋物線”過點N,如果存在,求出M點坐標;不存在,說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
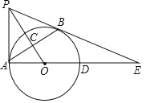
【題目】如圖,PA與⊙O相切于點A,過點A作AB⊥OP,垂足為C,交⊙O于點B.連接PB,AO,并延長AO交⊙O于點D,與PB的延長線交于點E.
(1)求證:PB是⊙O的切線;
(2)若OC=3,AC=4,求PB的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為落實“綠水青山就是金山銀山”的發展理念,某市政部門招標一工程隊負責在山腳下修建一座水庫的土方施工任務.該工程隊有![]() 兩種型號的挖掘機,已知3臺
兩種型號的挖掘機,已知3臺![]() 型和5臺
型和5臺![]() 型挖掘機同時施工一小時挖土165立方米;4臺
型挖掘機同時施工一小時挖土165立方米;4臺![]() 型和7臺
型和7臺![]() 型挖掘機同時施工一小時挖土225立方米.每臺
型挖掘機同時施工一小時挖土225立方米.每臺![]() 型挖掘機一小時的施工費用為300元,每臺
型挖掘機一小時的施工費用為300元,每臺![]() 型挖掘機一小時的施工費用為180元.
型挖掘機一小時的施工費用為180元.
(1)分別求每臺![]() 型,
型, ![]() 型挖掘機一小時挖土多少立方米?
型挖掘機一小時挖土多少立方米?
(2)若不同數量的![]() 型和
型和![]() 型挖掘機共12臺同時施工4小時,至少完成1080立方米的挖土量,且總費用不超過12960元.問施工時有哪幾種調配方案,并指出哪種調配方案的施工費用最低,最低費用是多少元?
型挖掘機共12臺同時施工4小時,至少完成1080立方米的挖土量,且總費用不超過12960元.問施工時有哪幾種調配方案,并指出哪種調配方案的施工費用最低,最低費用是多少元?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,![]() 是直角三角形,
是直角三角形,![]() .
.
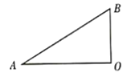
(1)請用尺規作圖法,作![]() ,使它與
,使它與![]() 相切于點
相切于點![]() ,與
,與![]() 相交于點
相交于點![]() ;保留作圖痕跡,不寫作法,請標明字母)
;保留作圖痕跡,不寫作法,請標明字母)
(2)在(1)的圖中,若![]() ,
,![]() ,求弧
,求弧![]() 的長.(結果保留
的長.(結果保留![]() )
)
查看答案和解析>>
科目:初中數學 來源: 題型:
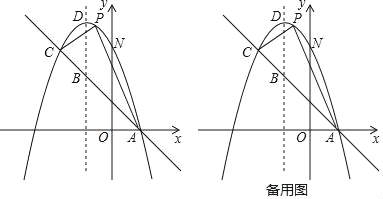
【題目】如圖,已知拋物線y=﹣x2+bx+c與一直線相交于A(1,0)、C(﹣2,3)兩點,與y軸交于點N,其頂點為D.
(1)求拋物線及直線AC的函數關系式;
(2)若P是拋物線上位于直線AC上方的一個動點,求△APC的面積的最大值及此時點P的坐標;
(3)在對稱軸上是否存在一點M,使△ANM的周長最小.若存在,請求出M點的坐標和△ANM周長的最小值;若不存在,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com