
【題目】某公交車每天的支出費用為60 元,每天的乘車人數 x(人)與每天利潤(利潤 =票款收入 -支出費用)y(元)的變化關系如下表所示(每位乘客的乘車票價固定不變):
x(人) | … | 200 | 250 | 300 | 350 | 400 | … |
y(元) | … | -20 | -10 | 0 | 10 | 20 | … |
根據表格中的數據,回答下列問題:
(1)在這個變化關系中,自變量是什么?因變量是什么?
(2)若要不虧本,該公交車每天乘客人數至少達到多少?
(3)請你判斷一天乘客人數為 5 00人時,利潤是多少?
(4) 試寫出該公交車每天利潤 y(元)與每天乘車人數x (人)的關系式.
【答案】(1)每天的乘車人數,每天的利潤;(3)300;(3)40;(4)y=![]() x-60.
x-60.
【解析】
(1)根據自變量、因變量的定義,結合題意即可解答;(2)觀察表格中的數據即可解答;(3)觀察表格中的數據可知,乘車人數每增加50人,每天的利潤增加10元,由此即可解答;(4)設每位乘客的公交票價為a元,根據題意得y=ax-60,在把x=200,y=-20代入y=ax-60,求得a的值,由此即可求得該公交車每天利潤y(元)與每天乘車人數x (人)的關系式.
(1)在這個變化過程中,每天的乘車人數是自變量,每天的利潤是因變量;
(2)根據表格可得:當每天乘車人數至少達到300人時,該公交車才不會虧損;
(3)觀察表格中的數據可知,乘車人數每增加50人,每天的利潤增加10元,
∴當每天的乘客人數為 5 00人時,利潤為40元.
(4)設每位乘客的公交票價為a元,
根據題意得:y=ax-60,
把x=200,y=-20代入y=ax-60,
得:200a-60=-20
解得:a=![]() ,
,
∴y=![]() x-60.
x-60.


科目:初中數學 來源: 題型:
【題目】某校七(1)班學生為了解某小區家庭月均用水情況,隨機調查了該小區部分家庭,并將調查數據進行如下整理,已知該小區用水量不超過![]() 的家庭占被調查家庭總數的百分比為12%,請根據以上信息解答下列問題:
的家庭占被調查家庭總數的百分比為12%,請根據以上信息解答下列問題:
級別 |
|
|
|
|
|
|
月均用水量 |
|
|
|
|
|
|
頻數(戶) | 6 | 12 |
| 10 | 4 | 2 |
(1)本次調查采用的方式是 (填“普查”或“抽樣調查”),樣本容量是 ;
(2)補全頻率分布直方圖;

(3)若將調查數據繪制成扇形統計圖,則月均用水量“![]() ”的圓心角度數是 .
”的圓心角度數是 .
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】甲口袋中放有3個紅球和5個白球,乙口袋中放有7個紅球和9個白球,所有球除顏色外都相同.充分攪勻兩個口袋,分別從兩個口袋中任意摸出一個球,設從甲中摸出紅球的概率是![]() (紅),從乙中摸出紅球的概率是
(紅),從乙中摸出紅球的概率是![]() (紅).
(紅).
(1)求![]() (紅)與
(紅)與![]() (紅)的值,并比較它們的大小.
(紅)的值,并比較它們的大小.
(2)將甲、乙兩個口袋的球都倒入丙口袋,充分攪勻后,設從丙中任意摸出一球是紅球的概率為![]() (紅).小明認為:
(紅).小明認為:![]() (紅)
(紅)![]()
![]() (紅)
(紅)![]()
![]() (紅).他的想法正確嗎?請說明理由.
(紅).他的想法正確嗎?請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知二次函數y=x2﹣2x﹣3與x軸交于A、B兩點(A在B的左邊),與y軸交于點C.
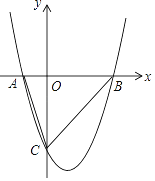
(1)求出點A、B、C的坐標.
(2)求S△ABC
(3)在拋物線上(除點C外),是否存在點N,使得S△NAB=S△ABC , 若存在,求出點N的坐標,若不 存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
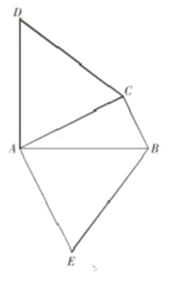
【題目】如圖,在△ABC中,DA⊥AB,AD=AB,EA⊥AC,AE=AC.
(1)試說明△ACD≌△AEB;
(2)若∠ACB=90°,連接CE,
①說明EC平分∠ACB;
②判斷DC與EB的位置關系,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,在菱形![]() 中,
中,![]() ,
,![]() ,點
,點![]() 是
是![]() 上一點,點
上一點,點![]() 在
在![]() 上,且
上,且![]() ,設
,設![]() .
.

(1)當![]() 時,如圖2,求
時,如圖2,求![]() 的長;
的長;

(2)設![]() ,求
,求![]() 關于
關于![]() 的函數關系式及其定義域;
的函數關系式及其定義域;
(3)若![]() 是以
是以![]() 為腰的等腰三角形,求
為腰的等腰三角形,求![]() 的長.
的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】列方程組或不等式解應用題
現有![]() ,
,![]() 兩種商品,買2件
兩種商品,買2件![]() 商品和1件
商品和1件![]() 商品用了80元,買4件
商品用了80元,買4件![]() 商品和3件
商品和3件![]() 商品用了180元
商品用了180元
(1)求![]() ,
,![]() 兩種商品每件各是多少元?
兩種商品每件各是多少元?
(2)如果小亮準備購買![]() ,
,![]() 兩種商品共10件,總費用不超過260元,至少買多少件
兩種商品共10件,總費用不超過260元,至少買多少件![]() 商品?
商品?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知![]() ,
,![]() ,且滿足
,且滿足![]() .
.


(1)求![]() 、
、![]() 兩點的坐標;
兩點的坐標;
(2)點![]() 在線段
在線段![]() 上,
上,![]() 、
、![]() 滿足
滿足![]() ,點
,點![]() 在
在![]() 軸負半軸上,連
軸負半軸上,連![]() 交
交![]() 軸的負半軸于點
軸的負半軸于點![]() ,且
,且![]() ,求點
,求點![]() 的坐標;
的坐標;
(3)平移直線![]() ,交
,交![]() 軸正半軸于
軸正半軸于![]() ,交
,交![]() 軸于
軸于![]() ,
,![]() 為直線
為直線![]() 上第三象限內的點,過
上第三象限內的點,過![]() 作
作![]() 軸于
軸于![]() ,若
,若![]() ,且
,且![]() ,求點
,求點![]() 的坐標.
的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖:拋物線y=ax2+bx+c交y軸于點C(0,4),對稱軸x=2與x軸交于點D,頂點為M,且DM=OC+OD,
(1)求拋物線的解析式;
(2)設點P(x,y)是第一象限內該拋物線上的一個動點,△PCD的面積為S,求S關于x的函數關系式,寫出自變量x的取值范圍,并求當x取多少時,S的值最大,最大是多少?

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com