
如果我們定義:“到三角形的兩個頂點距離相等的點,叫做此三角形的開心點。”那么:
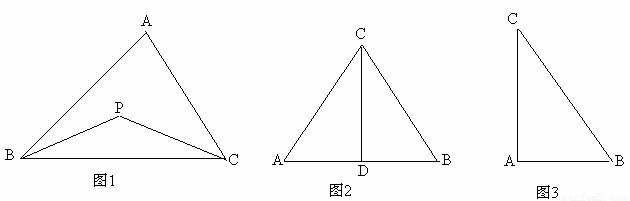
(1)如圖1,觀察并思考,△ABC的開心點有 個
(2)如圖2,CD為等邊三角形ABC的高,開心點P在高CD上,且PD=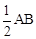 ,則∠APB的度數為
,則∠APB的度數為
(3)已知△ABC為直角三角形,斜邊BC=5,AB=3,開心點P在AC邊上,試探究PA的長。
(1)無數;(2)90°;(3)2或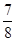 .
.
【解析】
試題分析:(1)根據線段垂直平分線的性質可知,△ABC的開心點有無數個;(2)連接PA、PB,根據開心點的定義,分①PB=PC,②PA=PC,③PA=PB三種情況利用等邊三角形的性質求出PD與AB的關系,然后判斷出只有情況③是合適的,再根據等腰直角三角形的性質求出∠APB=45°,然后即可求出∠APB的度數;(3)先根據勾股定理求出AC的長度,根據開心點的定義,分①PB=PC,②PA=PC,③PA=PB三種情況,根據三角形的性質計算即可得解.
試題解析:(1)無數.
(2)①若PB=PC,連接PB,則∠PCB=∠PBC,
∵CD為等邊三角形的高,∴AD=BD,∠PCB=30°.
∴∠PBD=∠PBC=30°,∴PD=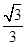 DB=
DB=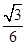 AB.與已知PD=
AB.與已知PD=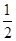 AB矛盾,∴PB≠PC.
AB矛盾,∴PB≠PC.
②若PA=PC,連接PA,同理可得PA≠PC.
③若PA=PB,由PD=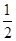 AB,得PD=AD =BD,∴∠APD=∠BPD=45°. ∴∠APB=90°.
AB,得PD=AD =BD,∴∠APD=∠BPD=45°. ∴∠APB=90°.
(3)∵BC=5,AB=3,∴AC=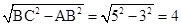 .
.
①若PB=PC,設PA=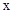 ,則
,則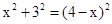 ,∴
,∴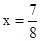 ,即PA=
,即PA=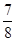 .
.
②若PA=PC,則PA=2.
③若PA=PB,由圖知,在Rt△PAB中,不可能.
∴PA=2或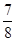 .
.

考點:1.新定義;2.線段垂直平分線的性質;3.等腰(邊)三角形的性質;4.勾股定理;5.分類思想的應用.


科目:初中數學 來源: 題型:
 如圖,點A在射線OP上,OA等于2cm.我們定義如下兩種操作
如圖,點A在射線OP上,OA等于2cm.我們定義如下兩種操作查看答案和解析>>
科目:初中數學 來源: 題型:解答題
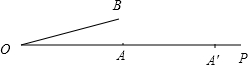 如圖,點A在射線OP上,OA等于2cm.我們定義如下兩種操作
如圖,點A在射線OP上,OA等于2cm.我們定義如下兩種操作查看答案和解析>>
科目:初中數學 來源: 題型:
如圖,點A在射線OP上,OA等于2cm.我們定義如下兩種操作:
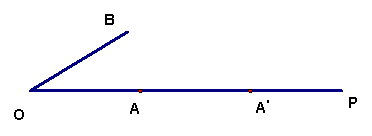
操作一 ![]() 旋轉操作,記為X操作:
旋轉操作,記為X操作:
OA繞點O按逆時針方向旋轉![]() 到OB,那么點B的位置可以用(2,
到OB,那么點B的位置可以用(2,![]() )表示;OB繞點O再按逆時針方向旋轉
)表示;OB繞點O再按逆時針方向旋轉![]() 到OC,那么點C的位置可以用(2,
到OC,那么點C的位置可以用(2,![]() )表示.
)表示.
操作二 線段加倍操作,記為Y操作:
如圖,如果延長OA到點![]() ,使
,使![]() =2
=2![]() ,那么點
,那么點![]() 的位置可以用(4,
的位置可以用(4,![]() )表示;如果延長OB到點
)表示;如果延長OB到點![]() ,使
,使![]() =2
=2![]() ,那么點
,那么點![]() 的位置可以用(4,
的位置可以用(4,![]() )表示.
)表示.
(1)現操作如下:
第一次對點A進行X操作,得到第一個點![]() ,其位置可以表示為( ,
,其位置可以表示為( , ![]() );
);
第二次對點![]() 進行Y操作,得到第二個點
進行Y操作,得到第二個點![]() ,其位置可以表示為( ,
,其位置可以表示為( , ![]() );
);
第三次對點![]() 進行X操作,得到第三個點
進行X操作,得到第三個點![]() ,其位置可以表示為( ,
,其位置可以表示為( , ![]() );
);
第四次對點![]() 進行Y操作,得到第四個點
進行Y操作,得到第四個點![]() ,其位置可以表示為( ,
,其位置可以表示為( , ![]() );
);
……,如此依次進行操作X、Y、X、Y、![]() ,可得到若干點.
,可得到若干點.
(2)按如上操作,若經過t次操作后得到A2010點,其位置表示為(p,q![]() ),則t、p、q的值分別為多少?
),則t、p、q的值分別為多少?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com