甲、乙、丙三位小朋友做寫1、2、3數字游戲,每人隨機寫出一個數字.解決下列問題:
(1)用適當的方法表示所有可能出現的結果有多少種?
(2)求三個人寫出相同數字的概率;
(3)求其中至少有兩個人寫的是數字“1”的概率是多少?
【答案】
分析:用樹狀圖分甲可能寫的數字,乙可能寫得到數字,丙可能寫的數字列舉出所有情況,看三個人寫出相同數字的情況數及至少兩個人寫的是數字“1”的情況數占所有情況數的多少即可.
解答:解:(1)共有27種可能出現的結果;
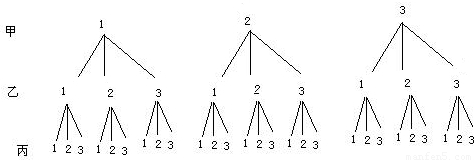
(2)三個人寫出相同數字的情況數是3,
∴P
(三人寫出數字都相同)=

=

;
(3)至少兩個人寫的是數字“1”的情況數是7,
∴P
(至少兩人是寫1)=

.
點評:本題考查了用列樹狀圖的方法解決概率問題,得到三個人寫出相同數字的情況數及至少兩個人寫的是數字“1”的情況數是解決本題的關鍵,用到的知識點為:概率等于所求情況數與總情況數之比.
