
【題目】某小麥改良品種后平均每公頃增加產量a噸,原來產m噸小麥的一塊土地,現在小麥的總產量增加了20噸.
(1)當a=0.8,m=100時,原來和現在小麥的平均每公頃產量各是多少?
(2)請直接接寫出原來小麥的平均每公頃產量是 噸,現在小麥的平均每公頃產量是 噸;(用含a、m的式于表示)
(3)在這塊土地上,小麥的改良品種成熟后,甲組收割完需n小時,乙組比甲組少用0.5小時就能收割完,求兩組一起收割完這塊麥田需要多少小時?
【答案】(1)原來和現在小麥的平均每公頃產量各是4噸,4.8噸;(2)![]() ,
,![]() ;(3)兩組一起收割完這塊麥田需要
;(3)兩組一起收割完這塊麥田需要![]() 小時.
小時.
【解析】
(1)設原來小麥平均每公頃產量是x噸,根據題意列出分式方程求解并驗根即可;(2)設原來小麥平均每公頃產量是y噸,根據題意列出分式方程求解并驗根即可;(3)由題意得知,工作總量為m+20,甲的工作效率為:![]() ,乙的工作效率為:
,乙的工作效率為:![]() ,再由工作總量除以甲乙的工作效率和即可得出工作時間.
,再由工作總量除以甲乙的工作效率和即可得出工作時間.
解:(1)設原來平均每公頃產量是x噸,則現在平均每公頃產量是(x+0.8)噸,
根據題意可得:![]()
解得:x=4,
檢驗:當x=4時,x(x+0.8)≠0,
∴原分式方程的解為x=4,
∴現在平均每公頃產量是4.8噸,
答:原來和現在小麥的平均每公頃產量各是4噸,4.8噸.
(2)設原來小麥平均每公頃產量是y噸,則現在玉米平均每公頃產量是(y+a)噸,
根據題意得:![]()
解得;y=![]() ,
,
經檢驗:y=![]() 是原方程的解,
是原方程的解,
則現在小麥的平均每公頃產量是:![]()
故答案為:![]() ,
,![]() ;
;
(3)根據題意得: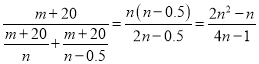
答:兩組一起收割完這塊麥田需要![]() 小時.
小時.


 黎明文化寒假作業系列答案
黎明文化寒假作業系列答案 寒假天地重慶出版社系列答案
寒假天地重慶出版社系列答案科目:初中數學 來源: 題型:
【題目】∠ACD是△ABC的外角,BE平分∠ABC,CE平分∠ACD,且BE、CE交于點E.
(1)若∠A=58,求:∠E的度數.
(2)猜想∠A與∠E的關系,并說明理由.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知矩形![]() 的邊
的邊![]() ,
,![]() ,現將矩形
,現將矩形![]() 如圖放在直線
如圖放在直線![]() 上,且沿著
上,且沿著![]() 向右作無滑動地翻滾,當它翻滾到位置
向右作無滑動地翻滾,當它翻滾到位置![]() 時,計算:
時,計算:
![]()
![]() 頂點
頂點![]() 所經過的路線長為________;
所經過的路線長為________;
![]() 點
點![]() 經過的路線與直線
經過的路線與直線![]() 所圍成的面積為________.
所圍成的面積為________.
查看答案和解析>>
科目:初中數學 來源: 題型:
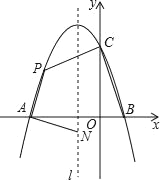
【題目】如圖,拋物線y=ax2+bx+c與x軸交于點A和點B(1,0),與y軸交于點C(0,3),其對稱軸l為x=﹣1.
(1)求拋物線的解析式并寫出其頂點坐標;
(2)若動點P在第二象限內的拋物線上,動點N在對稱軸l上.
①當PA⊥NA,且PA=NA時,求此時點P的坐標;
②當四邊形PABC的面積最大時,求四邊形PABC面積的最大值及此時點P的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某工廠準備用圖甲所示的A型正方形板材和B型長方形板材,制作成圖乙所示的豎式和橫式兩種無蓋箱子.
(1)若該工廠準備用不超過10000元的資金去購買A,B兩種型號板材,并全部制作豎式箱子,已知A型板材每張30元,B型板材每張90元,求最多可以制作豎式箱子多少只?
(2)若該工廠倉庫里現有A型板材65張、B型板材110張,用這批板材制作兩種類型的箱子,問制作豎式和橫式兩種箱子各多少只,恰好將庫存的板材用完?
(3)若該工廠新購得65張規格為3×3m的C型正方形板材,將其全部切割成A型或B型板材(不計損耗),用切割成的板材制作兩種類型的箱子,要求豎式箱子不少于20只,且材料恰好用完,則能制作兩種箱子共 只.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知二次函數![]() 的圖象如圖所示,則下列結論:①ac>0;②a-b+c<0;
的圖象如圖所示,則下列結論:①ac>0;②a-b+c<0;![]() 當
當![]() 時,
時,![]() ;
;![]() ,其中錯誤的結論有
,其中錯誤的結論有![]()
![]()
A. ②③ B. ②④ C. ①③ D. ①④
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】拋物線y=x2﹣2x﹣3與交y軸負半軸于C點,直線y=kx+2交拋物線于E、F兩點(E點在F點左邊).使△CEF被y軸分成的兩部分面積差為5,則k的值為_____.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com