
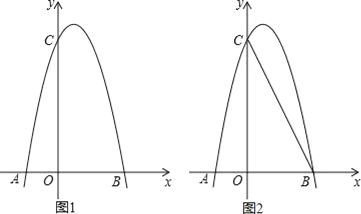
【題目】如圖1,對稱軸為直線x=![]() 的拋物線經過B(2,0)、C(0,4)兩點,拋物線與x軸的另一交點為A
的拋物線經過B(2,0)、C(0,4)兩點,拋物線與x軸的另一交點為A
(1)求拋物線的解析式;
(2)若點P為第一象限內拋物線上的一點,設四邊形COBP的面積為S,求S的最大值;
(3)如圖2,若M是線段BC上一動點,在x軸是否存在這樣的點Q,使△MQC為等腰三角形且△MQB為直角三角形?若存在,求出點Q的坐標;若不存在,請說明理由.
【答案】(1)![]() ;(2)6;(3)Q(
;(2)6;(3)Q(![]() ,0)或Q(
,0)或Q(![]() ,0).
,0).
【解析】試題分析:(1)由對稱軸的對稱性得出點A的坐標,由待定系數法求出拋物線的解析式;
(2)作輔助線把四邊形COBP分成梯形和直角三角形,表示出面積S,化簡后是一個關于S的二次函數,求最值即可;
(3)畫出符合條件的Q點,只有一種,①利用平行相似得對應高的比和對應邊的比相等列比例式;②在直角△OCQ和直角△CQM利用勾股定理列方程;兩方程式組成方程組求解并取舍.
試題解析:(1)由對稱性得:A(﹣1,0),設拋物線的解析式為:y=a(x+1)(x﹣2),把C(0,4)代入:4=﹣2a,a=﹣2,∴y=﹣2(x+1)(x﹣2),∴拋物線的解析式為: ![]() ;
;
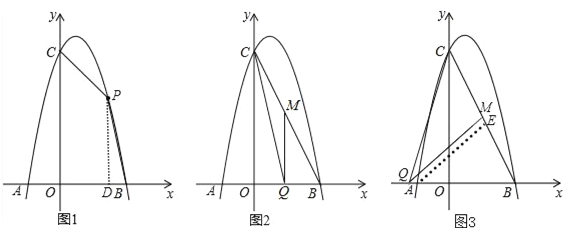
(2)如圖1,設點P(m, ![]() ),過P作PD⊥x軸,垂足為D,∴S=S梯形+S△PDB=
),過P作PD⊥x軸,垂足為D,∴S=S梯形+S△PDB=![]() ,∴S=
,∴S=![]() =
=![]() ,∵﹣2<0,∴S有最大值,則S大=6;
,∵﹣2<0,∴S有最大值,則S大=6;
(3)存在這樣的點Q,使△MQC為等腰三角形且△MQB為直角三角形,理由是:
分以下兩種情況:
①當∠BQM=90°時,如圖2:
∵∠CMQ>90°,∴只能CM=MQ.
設直線BC的解析式為:y=kx+b,把B(2,0)、C(0,4)代入得: ![]() ,解得:
,解得: ![]() ,∴直線BC的解析式為:y=﹣2x+4,,∴直線BC的解析式為:y=﹣2x+4,設M(m,﹣2m+4),則MQ=﹣2m+4,OQ=m,BQ=2﹣m,在Rt△OBC中,BC=
,∴直線BC的解析式為:y=﹣2x+4,,∴直線BC的解析式為:y=﹣2x+4,設M(m,﹣2m+4),則MQ=﹣2m+4,OQ=m,BQ=2﹣m,在Rt△OBC中,BC=![]() =
=![]() =
=![]() ,∵MQ∥OC,∴△BMQ∽BCO,∴
,∵MQ∥OC,∴△BMQ∽BCO,∴![]() ,即
,即![]() ,∴BM=
,∴BM=![]() =
= ![]() ,∴CM=BC﹣BM=
,∴CM=BC﹣BM=![]() =
= ![]() ,∵CM=MQ,∴﹣2m+4=
,∵CM=MQ,∴﹣2m+4= ![]() ,m=
,m=![]() =
=![]() ,∴Q(
,∴Q(![]() ,0).
,0).
②當∠QMB=90°時,如圖3:
設M(a,﹣2a+4),過A作AE⊥BC,垂足為E,則AE的解析式為: ![]() ,則直線BC與直線AE的交點E(1.4,1.2),設Q(﹣x,0)(x>0),∵AE∥QM,∴△ABE∽△QBM,∴
,則直線BC與直線AE的交點E(1.4,1.2),設Q(﹣x,0)(x>0),∵AE∥QM,∴△ABE∽△QBM,∴![]() ①,由勾股定理得:
①,由勾股定理得: ![]() ②,由①②得:
②,由①②得: ![]() =4(舍),
=4(舍),![]() =
=![]() ,當a=
,當a=![]() 時,x=
時,x=![]() ,∴Q(
,∴Q(![]() ,0).
,0).
綜上所述,Q點坐標為(![]() ,0)或(
,0)或(![]() ,0).
,0).


 A加金題 系列答案
A加金題 系列答案 全優測試卷系列答案
全優測試卷系列答案科目:初中數學 來源: 題型:
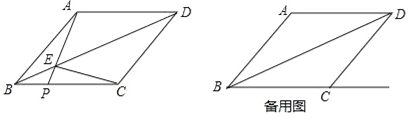
【題目】已知:如圖,在菱形ABCD中,AB=5,聯結BD,sin∠ABD=![]() .點P是射線BC上的一個動點(點P不與點B重合),聯結AP,與對角線BD相交于點E,聯結EC.
.點P是射線BC上的一個動點(點P不與點B重合),聯結AP,與對角線BD相交于點E,聯結EC.
(1)求證:AE=CE;
(2)當點P在線段BC上時,設BP=x,△PEC的面積為y,求y關于x的函數解析式,并寫出它的定義域;
(3)當點P在線段BC的延長線上時,若△PEC是直角三角形,求線段BP的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知正比例函數y1=kx的圖象與反比例函數![]() (k為常數,k≠5且k≠0)的圖象有一個交點的橫坐標是2.
(k為常數,k≠5且k≠0)的圖象有一個交點的橫坐標是2.
(1)求這兩個函數的解析式;
(2)求這兩個函數圖象的交點坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某公司銷售部有營銷人員15人,銷售部為了制定某種商品的月銷售定額,統計了這15人某月的銷售量如下:

【1】求這15位營銷人員該月銷售量的平均數、中位數、眾數
【2】假設銷售部負責人把每個營銷人員的月銷售量定為320件,你認為是否合理,為什么?如果不合理,請你制定一個較為合理的銷售定額,并說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】永州70年的發展歷程,是一幅波瀾壯闊的歷史畫卷.保持了經濟社會穩中有進,進中向好的發展態勢,城鄉居民人均可支配收入持續增長.截至2019年底,全市人口56萬人,把56萬這個數用科學記數法表示為( )
A.0.56×106B.5.6×104C.5.6×105D.5.6×106
查看答案和解析>>
科目:初中數學 來源: 題型:
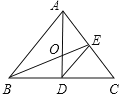
【題目】如圖,△ABC的角平分線AD、中線BE相交于點O,則①AO是△ABE的角平分線;②BO是△ABD的中線;③DE是△ADC的中線;④ED是△EBC的角平分線的結論中正確的有_________個.
查看答案和解析>>
科目:初中數學 來源: 題型:
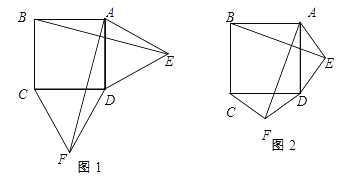
【題目】如圖1,在正方形ABCD的外側,作兩個等邊三角形ADE和DCF,連接AF,BE.
(Ⅰ)請寫出AF與BE的數量關系與位置關系分別是什么,并證明.
(Ⅱ)如圖2,若將條件“兩個等邊三角形ADE和DCF”變為兩個等腰三角形ADE和DCF,且EA=ED=FD=FC,第(1)問中的結論是否仍然成立?請作出判斷并給予證明;
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com