
 E=2,點F在BC邊上,EF與邊AD相交于點G,DF⊥EF,設AG=x,DF=y.
E=2,點F在BC邊上,EF與邊AD相交于點G,DF⊥EF,設AG=x,DF=y.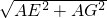 =
= ,
, =
= ,
,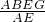 =
=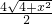 =
=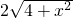 ,
,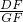 =
= ,
,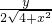 =
= ,
,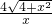 ,定義域為0<x≤4.
,定義域為0<x≤4. =
=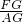 ,
,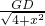 =
=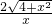 ,
,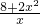 .
.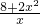 =11,x1=1,x2=
=11,x1=1,x2= ,
, .
. ,⊙F的半徑FD=
,⊙F的半徑FD= .
. =
=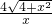 -
- ,
, ≠0,
≠0,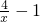 ,
, =
= ,⊙F的半徑FD=
,⊙F的半徑FD= ,
, ,⊙F的半徑為4
,⊙F的半徑為4 ;或⊙E的半徑為
;或⊙E的半徑為 ,⊙F的半徑為4
,⊙F的半徑為4 .
. =
= ,進而可得到關于x、y的關系式,由二次根式有意義的條件求出x的取值范圍即可;
,進而可得到關于x、y的關系式,由二次根式有意義的條件求出x的取值范圍即可; =
=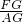 ,可用x表示出GD的值,再把AD=11代入即可求出x的值,進而得出AG的長;
,可用x表示出GD的值,再把AD=11代入即可求出x的值,進而得出AG的長;

科目:初中數學 來源: 題型:
 (2013•赤峰)如圖,在Rt△ABC中,∠B=90°,AC=60cm,∠A=60°,點D從點C出發沿CA方向以4cm/秒的速度向點A勻速運動,同時點E從點A出發沿AB方向以2cm/秒的速度向點B勻速運動,當其中一個點到達終點時,另一個點也隨之停止運動.設點D、E運動的時間是t秒(0<t≤15).過點D作DF⊥BC于點F,連接DE,EF.
(2013•赤峰)如圖,在Rt△ABC中,∠B=90°,AC=60cm,∠A=60°,點D從點C出發沿CA方向以4cm/秒的速度向點A勻速運動,同時點E從點A出發沿AB方向以2cm/秒的速度向點B勻速運動,當其中一個點到達終點時,另一個點也隨之停止運動.設點D、E運動的時間是t秒(0<t≤15).過點D作DF⊥BC于點F,連接DE,EF.查看答案和解析>>
科目:初中數學 來源: 題型:
 如圖,在Rt△ABC中,∠BAC=90°,將△ABC沿線段BC向右平移得到△DEF,使CE=AE,連結AD、AE、CD,則下列結論:①AD∥BE且AD=BE;②∠ABC=∠DEF;③ED⊥AC;④四邊形AECD為菱形,其中正確的共有( )
如圖,在Rt△ABC中,∠BAC=90°,將△ABC沿線段BC向右平移得到△DEF,使CE=AE,連結AD、AE、CD,則下列結論:①AD∥BE且AD=BE;②∠ABC=∠DEF;③ED⊥AC;④四邊形AECD為菱形,其中正確的共有( )查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com