
三個小球上分別標有-2,0,1三個數,這三個球除了標的數不同外,其余均相同.將
小球放入一個不透明的布袋中攪勻.
(1)從布袋中任意摸出一個小球,將小球上所標之數記下,然后將小球放回袋中,攪勻后再任意摸
出一個小球,再記下小球上所標之數.求兩次記下之數的和大于0的概率.(請用“畫樹狀圖”或“列表”等方法給出分析過程,并求出結果)
(2)從布袋中任意摸出一個小球,將小球上所標之數記下,然后將小球放回袋中,攪勻后再任意摸出一個小球,將小球上所標之數再記下,…,這樣一共摸了13次.若記下的13個數之和等于-4,平方和等于14,求:這13次摸球中,摸到球上所標之數是0的次數.
科目:初中數學 來源: 題型:
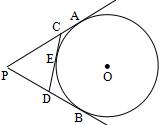
如圖,PA、PB切⊙O于A、B兩點,CD切⊙O于點E交PA、PB于C、D,若⊙O的半徑為r,PCD的周長等于3r,則tan∠APB的值是( )
A.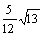 B.
B.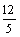
C.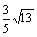 D.
D.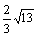
查看答案和解析>>
科目:初中數學 來源: 題型:
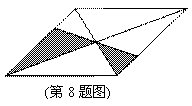
小明把如圖所示的平行四邊形紙板掛在墻上,玩飛鏢游戲(每次飛鏢均落在紙板上,且落在紙板的任何一個點的機會都相等),則飛鏢
落在陰影區域的概率是( )
A.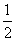 B.
B.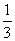 C.
C.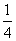 D.
D.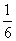
 |
查看答案和解析>>
科目:初中數學 來源: 題型:
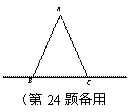
【探究發現】如圖1, 是等邊三角形,
是等邊三角形, ,EF交等邊三角形外角平分線CF所在的直線于點F.當點E是BC的中點時,有AE=EF成立;
,EF交等邊三角形外角平分線CF所在的直線于點F.當點E是BC的中點時,有AE=EF成立;
【數學思考】某數學興趣小組在探究AE、EF的關系時,運用“從特殊到一般”的數學思想,通過驗證得出如下結論:當點E是直線BC上(B,C除外)任意一點時(其它條件不變),結論AE=EF仍然成立.
假如你是該興趣小組中的一員,請你從“點E是線段BC上的任 意一點”;“點E是線段BC延長線上的任意一點”;“ 點E是線段BC反向延長線上的任意一點”三種情況中,任選一種情況,在備用圖1中畫出圖形,并進行證明.
意一點”;“點E是線段BC延長線上的任意一點”;“ 點E是線段BC反向延長線上的任意一點”三種情況中,任選一種情況,在備用圖1中畫出圖形,并進行證明.
 | |||
 | |||

【拓展應用】當點E在線段BC的延長線上時,若CE = BC,在備用圖2中畫出圖形,并運用上述結論求出 的值.
的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
如圖,已知在Rt△OAC中,O為坐標原點,直角頂點C在x軸的正半軸上,反比例函數y=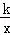 (k≠0)在第一象限的圖象經過OA的中點B,交AC于點D,連接OD.若△OCD∽△ACO,則直線OA的解析式為 .
(k≠0)在第一象限的圖象經過OA的中點B,交AC于點D,連接OD.若△OCD∽△ACO,則直線OA的解析式為 .
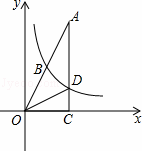
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com