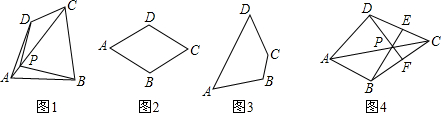
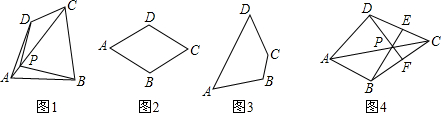
解:(1)如圖2,點P即為所畫點;
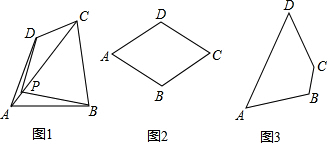
(2)如圖3,點P即為所作點(作法不唯一);
作法:①連接BD,
②作BD的垂直平分線,交AC的延長線于點P,
則點P即為所作點.
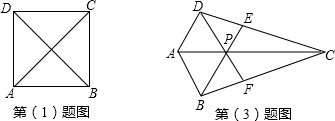
(3)連接DB.
在△DCF與△BCE中,
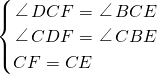
,
∴△DCF≌△BCE(AAS),
∴CD=CB,
∴∠CDB=∠CBD,
∴∠PDB=∠PBD,
∴PD=PB,
∵PA≠PC,
∴點P是四邊形ABCD的準等距點.
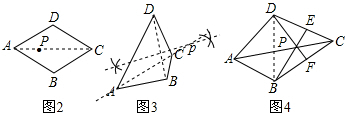
(4)①當四邊形的對角線互相垂直且任何一條對角線不平分另一對角線或者對角線互相平分且不垂直時,準等距點的個數為0個;
②當四邊形的對角線不互相垂直,又不互相平分,且有一條對角線的中垂線經過另一對角線的中點時,準等距點的個數為1個;
③當四邊形的對角線既不互相垂直又不互相平分,且任何一條對角線的中垂線都不經過另一條對角線的中點時,準等距點的個數為2個;
④四邊形的對角線互相垂直且至少有一條對角線平分另一對角線時,準等距點有無數個.
故答案為:0,1,2,無數.
分析:(1)根據菱形的對角線互相垂直平分,根據線段垂直平分線的性質,則只需要在其中一條對角線上找到和對角線的交點不重合的點即可;
(2)根據到線段兩個端點距離相等的點在線段的垂直平分線上,則可作對角線BD的垂直平分線和另一條對角線所在的直線的交點即為所求作;
(3)只需說明PD=PB即可.根據已知的條件可以根據AAS證明△DCF≌△BCE,則∠CDB=∠CBD,進而得到∠PDB=∠PBD,證明結論即可;
(4)根據上述確定準等距點的方法:即作其中一條對角線的垂直平分線和另一條對角線所在的直線的交點.所以分析討論的時候,主要是根據兩條對角線的位置關系進行分析討論.
點評:此題考查了菱形的性質、全等三角形的判定與性質、線段垂直平分線的性質等知識.此題屬于閱讀性題目,解題的關鍵是熟悉菱形的性質,能夠根據線段垂直平分線的性質的逆定理進行分析作圖,能夠根據找準等距點的方和四邊形中兩條對角線的位置關系判斷準等距點的個數.

 解:(1)如圖2,點P即為所畫點;
解:(1)如圖2,點P即為所畫點;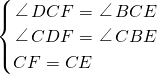 ,
,

 名校課堂系列答案
名校課堂系列答案