
【題目】閱讀下列兩則材料,回答問題:
材料一:因為![]() 所以我們將
所以我們將![]() 與
與![]() 稱為一対“有理化因式”,有時我們可以通過構造“有理化因式”求值
稱為一対“有理化因式”,有時我們可以通過構造“有理化因式”求值
例如:已知![]() ,求
,求![]() 的值
的值
解:![]() ,∵
,∵![]()
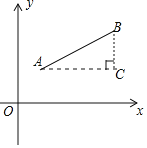
材料二:如圖,點A(x1,y1),點B(x2,y2),所以AB為斜邊作Rt△ABC,則C(x2,y1),于是AC=|x1﹣x2|,BC=|y1﹣y2|,所以AB=![]() ,反之,可將代數式
,反之,可將代數式![]() 的值看作點(x1,y1)到點(x2,y2)的距離.例如
的值看作點(x1,y1)到點(x2,y2)的距離.例如![]() =
=![]() ,所以可將代數式
,所以可將代數式![]() 的值看作點(x,y)到點(1,﹣1)的距離;
的值看作點(x,y)到點(1,﹣1)的距離;
(1)利用材料一,解關于x的方程:![]() ,其中x≤2;
,其中x≤2;
(2)利用材料二,求代數式![]() 的最小值,并求出此時y與x的函數關系式,寫出x的取值范圍.
的最小值,并求出此時y與x的函數關系式,寫出x的取值范圍.
【答案】(1)x=﹣2;(2)y=x+5(﹣3≤x≤1).
【解析】
(1)根據材料一類比計算![]() 的值,利用換元法解方程,可得結論;
的值,利用換元法解方程,可得結論;
(2)把根式下的式子轉化成平方+平方的形式,轉化成點到點的距離問題,根據兩點之間距離最短,所以當三個點共線時距離最短,可以求出最小值和函數關系式.
解:(1)![]() ,
,
![]() ,
,
![]() ;
;
設![]() ,
,
則![]() ,解得:
,解得:![]() ,
,
∴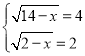 ,
,
∵x≤2,
解得:x=﹣2;
(2)![]() ,
,
![]() ,
,
![]()
![]() ,
,
所以可將![]() 看作點(x,y)到點(1,6)的距離;
看作點(x,y)到點(1,6)的距離;
可將![]() 看作點(x,y)到點(﹣3,2)的距離;
看作點(x,y)到點(﹣3,2)的距離;
∴當代數式![]() 取最小值,
取最小值,
即點(x,y)與點(1,6),(﹣3,2)在同一條直線上,并且點(x,y)位于點(1,6)、(﹣3,2)的中間,
∴![]() 的最小值=
的最小值=![]() ,且﹣3≤x≤1,
,且﹣3≤x≤1,
設過(x,y),(1,6),(﹣3,2)的直線解析式為:y=kx+b,
∴![]() ,
,
解得:![]() ,
,
∴y=x+5(﹣3≤x≤1).


科目:初中數學 來源: 題型:
【題目】如圖,在四邊形ABCD中,AB∥CD,∠B=90°,AB=12cm,AD=CD=8cm,動點E從點A出發沿AB以每秒1cm的速度向點B運動,動點F從點B出發沿BA以每秒1cm的速度向點A運動,過點E作AB的垂線交折線AD-DC于點G,以EG、EF為鄰邊作矩形EFHG,設點E、F運動的時間為t(秒),矩形EFHG與四邊形ABCD重疊部分的面積為S(cm2).
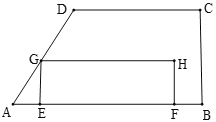
(1)求EG的長(用含t的代數式表示);
(2)當t為何值時,點G與點D重合?
(3)當點G在DC上時,求S(cm2)與t(秒)的函數關系式(S>0);
(4)連接EH、GF、AC、BD,在運動過程中,當這四條線段所在的直線有兩條平行時,直接寫出t的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
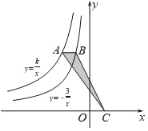
【題目】如圖,點A是反比例函數y=![]() 圖象上一點,過點A作x軸的平行線交反比例函數y=﹣
圖象上一點,過點A作x軸的平行線交反比例函數y=﹣![]() 的圖象于點B,點C在x軸上,且S△ABC=
的圖象于點B,點C在x軸上,且S△ABC=![]() ,則k=( )
,則k=( )
A. 6B. ﹣6C. ![]() D. ﹣
D. ﹣![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
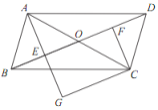
【題目】如圖,在□ABCD 中,對角線 AC 與 BD 相交于點 O ,點 E , F 分別為 OB , OD 的中點,延長 AE 至 G ,使 EG =AE ,連接 CG .
(1)求證: △ABE≌△CDF ;
(2)當 AB 與 AC 滿足什么數量關系時,四邊形 EGCF 是矩形?請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某公司銷售一種新型節能產品,現準備從國內和國外兩種銷售方案中選擇一種進行銷售.若只在國內銷售,銷售價格y(元/件)與月銷量x(件)的函數關系式為y=![]() x+150,成本為20元/件,無論銷售多少,每月還需支出廣告費62500元,設月利潤為w內(元).若只在國外銷售,銷售價格為150元/件,受各種不確定因素影響,成本為a元/件(a為常數,10≤a≤40),當月銷量為x(件)時,每月還需繳納
x+150,成本為20元/件,無論銷售多少,每月還需支出廣告費62500元,設月利潤為w內(元).若只在國外銷售,銷售價格為150元/件,受各種不確定因素影響,成本為a元/件(a為常數,10≤a≤40),當月銷量為x(件)時,每月還需繳納![]() x2元的附加費,設月利潤為w外(元).
x2元的附加費,設月利潤為w外(元).
(1)當x=1000時,y= 元/件,w內= 元;
(2)分別求出w內,w外與x間的函數關系式(不必寫x的取值范圍);
(3)當x為何值時,在國內銷售的月利潤最大?若在國外銷售月利潤的最大值與在國內銷售月利潤的最大值相同,求a的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】我市某中學學生會在開展“厲行勤儉節約,反對鋪張浪費”的主題教育活動中,在全校范圍內隨機抽取了若干名學生就某日晚飯浪費飯菜情況進行調查,調查內容分為四種:A.飯和菜全部吃完;B.有剩飯但菜吃完;C.飯吃完但菜有剩;D.飯和菜都有剩.學生會根據統計結果,繪制了如下統計表:根據所給信息,回答下列問題:
選項 | 頻數 | 頻率 |
A | 36 | m |
B | n | 0.2 |
C | 6 | 0.1 |
D | 6 | 0.1 |
(1)統計表中:m=______;n=______.
(2)該中學有1800名學生晚飯在校就餐,根據調查結果,估計當天晚飯有多少人能夠把飯和菜全部吃完?
(3)為了對同學們浪費的行為進行糾正,校學生會從飯和菜都有剩的甲、乙、丙、丁四名同學中任取2位同學進行批評教育,請用列表法或樹狀圖法求恰好抽到甲和丁的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為發展學生的核心素養,培養學生的綜合能力,某學校計劃開設四門選修課:樂器、舞蹈、繪畫、書法,學校采取隨機抽樣的方法進行問卷調查![]() 每個被調查的學生必須選擇而且只能選擇其中一門
每個被調查的學生必須選擇而且只能選擇其中一門![]() 對調查結果進行整理,繪制成如下兩幅不完整的統計圖
對調查結果進行整理,繪制成如下兩幅不完整的統計圖![]() 請結合圖中所給信息解答下列問題:
請結合圖中所給信息解答下列問題:


![]() 本次調查的學生共有______人,在扇形統計圖中,m的值是______.
本次調查的學生共有______人,在扇形統計圖中,m的值是______.
![]() 分別求出參加調查的學生中選擇繪畫和書法的人數,并將條形統計圖補充完整.
分別求出參加調查的學生中選擇繪畫和書法的人數,并將條形統計圖補充完整.
![]() 該校共有學生2000人,估計該校約有多少人選修樂器課程?
該校共有學生2000人,估計該校約有多少人選修樂器課程?
查看答案和解析>>
科目:初中數學 來源: 題型:
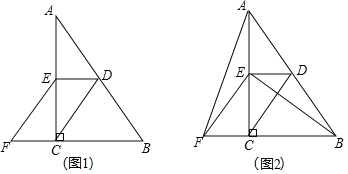
【題目】已知:如圖,在![]() 中,
中,![]() ,點D、E分別是AB、AC的中點,點F在BC延長線上,連接EF,且
,點D、E分別是AB、AC的中點,點F在BC延長線上,連接EF,且![]() .
.
![]() 如圖1,求證:四邊形CDEF是平行四邊形;
如圖1,求證:四邊形CDEF是平行四邊形;
![]() 如圖2,連接AF、BE,在不添加任何輔助線的情況下,請直接寫出圖2中所有與
如圖2,連接AF、BE,在不添加任何輔助線的情況下,請直接寫出圖2中所有與![]() 面積相等的三角形.
面積相等的三角形.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在一次數學綜合實踐活動中,小明計劃測量城門大樓的高度,在點B處測得樓頂A的仰角為22°,他正對著城樓前進21米到達C處,再登上3米高的樓臺D處,并測得此時樓頂A的仰角為45°.
(1)求城門大樓的高度;
(2)每逢重大節日,城門大樓管理處都要在A,B之間拉上繩子,并在繩子上掛一些彩旗,請你求出A,B之間所掛彩旗的長度(結果保留整數).(參考數據:sin22°≈![]() ,cos22°≈
,cos22°≈![]() ,tan22°≈
,tan22°≈![]() )
)

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com