
【題目】如圖,正方形ABCD是一塊綠化帶,陰影部分EOFB,GHMN都是正方形的花圃,其中EOFB的頂點O是正方形中心.已知自由飛翔的小鳥,將隨機落在這塊綠化帶上,則小鳥落在花圃上的概率為( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】C
【解析】設正方形ABCD的邊長為a,根據正方形的性質∠ACB=∠ACD=45°,AC=![]() a,再利用四邊形BEOF為正方形易得CF=OF=BF=
a,再利用四邊形BEOF為正方形易得CF=OF=BF=![]() a,則S正方形BEOF=
a,則S正方形BEOF=![]() a2,設正方形MNGH的邊長為x,易得CM=AN=MN=x,即3x=
a2,設正方形MNGH的邊長為x,易得CM=AN=MN=x,即3x=![]() a,解得x=
a,解得x=![]() a,則S正方形MNGH=
a,則S正方形MNGH=![]() a2,然后根據幾何概率的意義,用兩個小正方形的面積和除以正方形ABCD的面積即可得到小鳥落在花圃上的概率,從而得到小鳥不落在花圃上的概率.
a2,然后根據幾何概率的意義,用兩個小正方形的面積和除以正方形ABCD的面積即可得到小鳥落在花圃上的概率,從而得到小鳥不落在花圃上的概率.
設正方形ABCD的邊長為a,
∵四邊形ABCD為正方形,
∴∠ACB=∠ACD=45°,AC=![]() a,
a,
∵四邊形BEOF為正方形,
∴CF=OF=BF,
∴S正方形BEOF=(![]() a)2=
a)2=![]() a2,
a2,
設正方形MNGH的邊長為x,
∵△ANG和△CMH都是等腰直角三角形,
∴CM=AN=MN=x,
∴3x=![]() a,解得x=
a,解得x=![]() a,
a,
∴S正方形MNGH=(![]() a)2=
a)2=![]() a2,
a2,
∴小鳥不落在花圃上的概率=(![]() a2+
a2+![]() a2 )÷a2=
a2 )÷a2=![]() .
.
故選C.


科目:初中數學 來源: 題型:
【題目】有一種節能型轎車的油箱加滿天然氣后,油箱中的剩余天然氣量![]() (升)與轎車行駛路程
(升)與轎車行駛路程![]() (千米)之間的關系如圖所示,根據圖象回答下列問題:
(千米)之間的關系如圖所示,根據圖象回答下列問題:
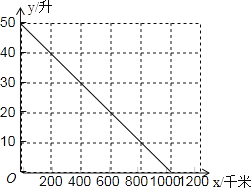
(1)這種轎車的油箱最多能裝______升天然氣,加滿天然氣后可供轎車行駛______千米.
(2)轎車每行駛200千米消耗天然氣________升.
(3)寫出![]() 與
與![]() 之間的函數關系式.
之間的函數關系式.
查看答案和解析>>
科目:初中數學 來源: 題型:
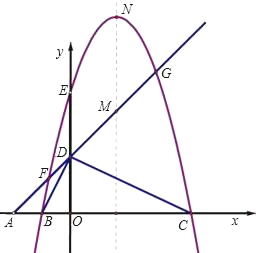
【題目】如圖,平面直角坐標系中,點A、B、C在x軸上,點D、E在y軸上,OA=OD=2,OC=OE=4,B為線段OA的中點,直線AD與經過B、E、C三點的拋物線交于F、G兩點,與其對稱軸交于M,點P為線段FG上一個動點(與F、G不重合),PQ∥y軸與拋物線交于點Q.
(1)求經過B、E、C三點的拋物線的解析式;
(2)判斷△BDC的形狀,并給出證明;當P在什么位置時,以P、O、C為頂點的三角形是等腰三角形,并求出此時點P的坐標;
(3)若拋物線的頂點為N,連接QN,探究四邊形PMNQ的形狀:①能否成為菱形;②能否成為等腰梯形?若能,請直接寫出點P的坐標;若不能,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】數軸是初中數學的一個重要工具,利用數軸可以將數與形完美地結合,研究數軸我們發現:若數軸上點A、點B表示的數分別為a、b,則A,B兩點之間的距離AB=|a﹣b|,線段AB的中點表示的數為![]() .如:如圖,數軸上點A表示的數為﹣2,點B表示的數為8,則A、兩點間的距離AB=|﹣2﹣8|=10,線段AB的中點C表示的數為
.如:如圖,數軸上點A表示的數為﹣2,點B表示的數為8,則A、兩點間的距離AB=|﹣2﹣8|=10,線段AB的中點C表示的數為![]() =3,點P從點A出發,以每秒3個單位長度的速度沿數軸向右勻速運動,同時點Q從點B出發,以每秒2個單位長度的速度向左勻速運動.設運動時間為t秒(t>0).
=3,點P從點A出發,以每秒3個單位長度的速度沿數軸向右勻速運動,同時點Q從點B出發,以每秒2個單位長度的速度向左勻速運動.設運動時間為t秒(t>0).
(1)用含t的代數式表示:t秒后,點P表示的數為 ,點Q表示的數為 .
(2)求當t為何值時,P、Q兩點相遇,并寫出相遇點所表示的數;
(3)求當t為何值時,PQ=![]() AB;
AB;
(4)若點M為PA的中點,點N為PB的中點,點P在運動過程中,線段MN的長度是否發生變化?若變化,請說明理由;若不變,請求出線段MN的長.
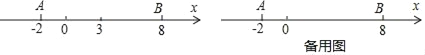
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知數軸上兩點A、B對應的數分別是 6,﹣8,M、N、P為數軸上三個動點,點M從A點出發速度為每秒2個單位,點N從點B出發速度為M點的3倍,點P從原點出發速度為每秒1個單位.
(1)若點M向右運動,同時點N向左運動,求多長時間點M與點N相距54個單位?
(2)若點M、N、P同時都向右運動,求多長時間點P到點M,N的距離相等?
![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
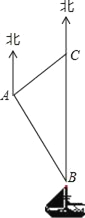
【題目】釣魚島是我國固有領土,現在我邊海漁民要在釣魚島附近進行捕魚作業,當漁船航行至B處時,測得該島位于正北方向20(1+![]() )海里的C處,為了防止某國海警干擾,請求我A處的魚監船前往C處護航,已知C位于A處的北偏東45°方向,A位于B的北偏西30°方向,求A、C之間的距離.
)海里的C處,為了防止某國海警干擾,請求我A處的魚監船前往C處護航,已知C位于A處的北偏東45°方向,A位于B的北偏西30°方向,求A、C之間的距離.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】解不等式組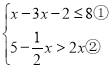 并求其整數解的和.
并求其整數解的和.
解:解不等式①,得_______;
解不等式②,得________;
把不等式①和②的解集在數軸上表示出來:
![]()
![]() 原不等式組的解集為________,
原不等式組的解集為________,
由數軸知其整數解為________,和為________.
在解答此題的過程中我們借助于數軸上,很直觀地找出了原不等式組的解集及其整數解,這就是“數形結合的思想”,同學們要善于用數形結合的思想去解決問題.
查看答案和解析>>
科目:初中數學 來源: 題型:
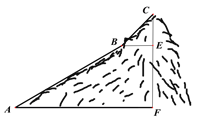
【題目】如圖,為測量一座山峰CF的高度,將此山的某側山坡劃分為AB和BC兩段,每一段山坡近似是“直”的,測得坡長AB=800米,BC=200米,斜坡AB的坡度![]() ,仰角∠CBE=50°.則山峰的高度CF約為( )米.(可用的參考數據:sin50°≈0.8,tan50°≈1.2,
,仰角∠CBE=50°.則山峰的高度CF約為( )米.(可用的參考數據:sin50°≈0.8,tan50°≈1.2, ![]() )
)
A. 500 B. 518 C. 530 D. 580
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某中學為了科學建設“學生健康成長工程”.隨機抽取了部分學生家庭對其家長進行了主題為“周末孩子在家您關心嗎?”的問卷調查,將回收的問卷進行分析整理,得到了如下的樣本統計表和扇形統計圖:
代號 | 情況分類 | 家庭數 |
| 帶孩子玩并且關心其作業完成情況 | 16 |
| 只關心其作業完成情況 | b |
| 只帶孩子玩 | 8 |
| 既不帶孩子玩也不關心其作業完成情況 | d |
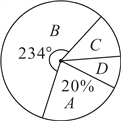
(1)求![]() 的值;
的值;
(2)該校學生家庭總數為500,學校決定按比例在![]() 類家庭中抽取家長組成培訓班,其比例為
類家庭中抽取家長組成培訓班,其比例為![]() 類取20%,
類取20%,![]() 類各取60%,請你估計該培訓班的家庭數;
類各取60%,請你估計該培訓班的家庭數;
(3)若在![]() 類家庭中只有一個城鎮家庭,其余是農村家庭,請用列舉法求出在
類家庭中只有一個城鎮家庭,其余是農村家庭,請用列舉法求出在![]() 類中隨機抽出2個家庭進行深度采訪,其中有一個是城鎮家庭的概率.
類中隨機抽出2個家庭進行深度采訪,其中有一個是城鎮家庭的概率.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com