
【題目】如圖,在平面直角坐標系![]() 中,已知直線
中,已知直線![]() 與反比例函數
與反比例函數![]() 的圖像交于點A,且點A的橫坐標為1,點B是x軸正半軸上一點,且
的圖像交于點A,且點A的橫坐標為1,點B是x軸正半軸上一點,且![]() ⊥
⊥![]() .
.

(1)求反比例函數的解析式;
(2)求點B的坐標;
(3)先在![]() 的內部求作點P,使點P到
的內部求作點P,使點P到![]() 的兩邊OA、OB的距離相等,且PA=PB.(不寫作法,保留作圖痕跡,在圖上標注清楚點P)
的兩邊OA、OB的距離相等,且PA=PB.(不寫作法,保留作圖痕跡,在圖上標注清楚點P)
【答案】(1)![]() ;(2)點
;(2)點![]() 的坐標是
的坐標是![]() ;(3)見解析.
;(3)見解析.
【解析】
(1)設點![]() 的坐標為(1,
的坐標為(1,![]() )先求出點A縱坐標,再求出反比例系數k即可得出反比例函數的解析式;
)先求出點A縱坐標,再求出反比例系數k即可得出反比例函數的解析式;
(2)過點A作AC⊥OB⊥,在RT△AOC中先求出OA,再在RT△AOB中求出OB即可解決問題;
(3)畫出∠AOB的平分線OM,線段AB的垂直平分線EF,OM與EF的交點就是所求的點P,設點P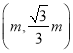 ,根據PA2=PB2,列出方程即可解決問題.
,根據PA2=PB2,列出方程即可解決問題.
解:(1)由題意,設點![]() 的坐標為(1,
的坐標為(1,![]() ),
),
∵點![]() 在正比例函數
在正比例函數![]() 的圖像上,
的圖像上,
∴![]() .
.
∴點![]() 的坐標為
的坐標為![]() .
.
∵點![]() 在反比例函數
在反比例函數![]() 的圖像上,
的圖像上,
∴![]() ,解得
,解得![]() .
.
∴反比例函數的解析式為![]() .
.
(2)過點![]() 作
作![]() ⊥
⊥![]() ,垂足為點
,垂足為點![]() ,
,
可得![]() ,
,![]() .
.
∵![]() ⊥
⊥![]() ,
,
∴∠![]() °.
°.
由勾股定理,得![]() .
.
∴![]() .
.
∴∠![]() °.
°.
∴∠![]() °.
°.
∵![]() ⊥
⊥![]() ,
,
∴∠![]() °.
°.
∴∠![]() °.
°.
∴![]() .
.
∴![]() .
.
∴點![]() 的坐標是
的坐標是![]() .
.
(3)如圖所示.

如圖作∠AOB的平分線OM,AB的垂直平分線EF,OM與EF的交點就是所求的點P,
∵∠POB=30°,
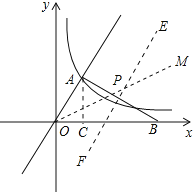
∴可以設點P坐標為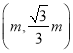 ,
,
∵PA2=PB2,

解得m=3,
∴點P的坐標是![]()


 名校課堂系列答案
名校課堂系列答案科目:初中數學 來源: 題型:
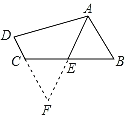
【題目】如圖,在四邊形ABCD中,AB∥CD,點E是BC的中點,若AE是∠BAD的平分線,試判斷AB,AD,DC之間的等量關系.解決此問題可以用如下方法:延長AE交DC的延長線于點F,從而把AB,AD,DC轉化在一個三角形中即可判斷.試探究AB,AD,DC之間的等量關系,并證明你的結論.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在正方形ABCD外取一點E,連接AE、BE、DE.過點A作AE的垂線交DE于點P.若AE=AP=1,PB=![]() ,下列結論:① △APD≌△AEB;② EB⊥ED;③ 點B到直線AE的距離為
,下列結論:① △APD≌△AEB;② EB⊥ED;③ 點B到直線AE的距離為![]() ; ④
; ④![]() ,其中正確結論的序號是( )
,其中正確結論的序號是( )
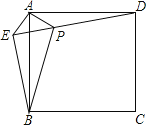
A. ①②③ B. ①②④ C. ①③④ D. ②③④
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知:如圖,AB是⊙O的直徑,AB=4,點F,C是⊙O上兩點,連接AC,AF,OC,弦AC平分∠FAB,∠BOC=60°,過點C作CD⊥AF交AF的延長線于點D,垂足為點D.
(1)求扇形OBC的面積(結果保留π);
(2)求證:CD是⊙O的切線.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知,如圖,在平面直角坐標系![]() 中,雙曲線
中,雙曲線![]() 與直線
與直線![]() 都經過點
都經過點![]() .
.

(1)求![]() 與
與![]() 的值;
的值;
(2)此雙曲線又經過點![]() ,點
,點![]() 是
是![]() 軸的負半軸上的一點,且點
軸的負半軸上的一點,且點![]() 到
到![]() 軸的距離是2 ,聯結
軸的距離是2 ,聯結![]() 、
、![]() 、
、![]() ,
,
①求![]() 的面積;
的面積;
②點![]() 在
在![]() 軸上,
軸上,![]() 為等腰三角形,請直接寫出點
為等腰三角形,請直接寫出點![]() 的坐標.
的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,在![]() 中,
中,![]() ,
,![]() ,AB=4,點
,AB=4,點![]() 是邊
是邊![]() 上動點(點
上動點(點![]() 不與點
不與點![]() 、
、![]() 重合),過點
重合),過點![]() 作
作![]() ,交
,交![]() 邊于點
邊于點![]() .
.

(1)求![]() 的大小;
的大小;
(2)若把![]() 沿著直線
沿著直線![]() 翻折得到
翻折得到![]() ,設
,設![]()
① 如圖2,當點![]() 落在斜邊
落在斜邊![]() 上時,求
上時,求![]() 的值;
的值;
② 如圖3,當點![]() 落在
落在![]() 外部時,
外部時,![]() 與
與![]() 相交于點
相交于點![]() ,如果
,如果![]() ,寫出
,寫出![]() 與
與![]() 的函數關系式以及定義域.
的函數關系式以及定義域.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】由一些大小相同,棱長為1的小正方體搭成的幾何體的俯視圖如圖所示,數字表示該位置的正方體個數.
(1)請畫出它的主視圖和左視圖;
(2)給這個幾何體噴上顏色(底面不噴色),需要噴色的面積為
(3)在不改變主視圖和俯視圖的情況下,最多可添加 塊小正方體.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】甲、乙兩名隊員參加射擊訓練,成績分別被制成下列兩個統計圖:
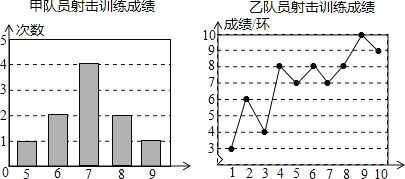
根據以上信息,整理分析數據如下:
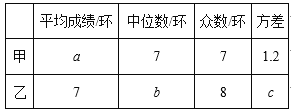
(1)寫出表格中a,b,c的值:a= ,b= ,c= .
(2)如果乙再射擊一次,命中7環,那么乙的射擊成績的方差 .(填“變大”“變小”“不變”)
(3)教練根據這10次成績若選擇甲參加比賽,教練的理由是什么?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】中日釣魚島爭端持續,我國海監船加大釣魚島海域的巡航維權力度.如圖,![]() ,
,![]() 海里,
海里,![]() 海里,釣魚島位于
海里,釣魚島位于![]() 點,我國海監船在點
點,我國海監船在點![]() 處發現有一不明國籍的漁船自
處發現有一不明國籍的漁船自![]() 點出發沿著
點出發沿著![]() 方向勻速駛向釣魚島所在地點
方向勻速駛向釣魚島所在地點![]() ,我國海監船立即從
,我國海監船立即從![]() 處出發以相同的速度沿某直線去攔截這艘漁船,結果在點
處出發以相同的速度沿某直線去攔截這艘漁船,結果在點![]() 處截住了漁船.
處截住了漁船.

(1)請用直尺和圓規作出![]() 處的位置.(不寫作法,保留作圖痕跡)
處的位置.(不寫作法,保留作圖痕跡)
(2)求我國海監船行駛的航程![]() 的長.
的長.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com