
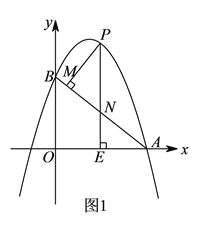
【題目】如圖![]() ,拋物線y=ax2-6ax+6(a≠0)與x軸交于點A(8,0),與y軸交于點B,在X軸上有一動點E(m,0)(0<m<8),過點E作x軸的垂線交直線AB于點N,交拋物線于點P,過點P作PM⊥AB于點M.
,拋物線y=ax2-6ax+6(a≠0)與x軸交于點A(8,0),與y軸交于點B,在X軸上有一動點E(m,0)(0<m<8),過點E作x軸的垂線交直線AB于點N,交拋物線于點P,過點P作PM⊥AB于點M.
(![]() )分別求出直線AB和拋物線的函數表達式;
)分別求出直線AB和拋物線的函數表達式;
(![]() )設△PMN的面積為S1,△AEN的面積為S2,若S1:S2=36:25,求m的值;
)設△PMN的面積為S1,△AEN的面積為S2,若S1:S2=36:25,求m的值;
(![]() )如圖2,在(
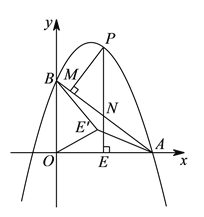
)如圖2,在(![]() )條件下,將線段OE繞點O逆時針旋轉得到OE',旋轉角為α(0°<α<90°),連接E'A、E'B.
)條件下,將線段OE繞點O逆時針旋轉得到OE',旋轉角為α(0°<α<90°),連接E'A、E'B.
①在x軸上找一點Q,使△OQE'∽△OE'A,并求出Q點的坐標;
②求BE'+![]() AE'的最小值.
AE'的最小值.
【答案】(1)![]() ;
; ![]() ;(2)4;(3)①
;(2)4;(3)①![]() ,②
,②![]() .
.
【解析】分析:(1)把點A(8,0)代入拋物線y=ax-6ax+6,可求得a的值,從而可得到拋物線的解析式,然后求得點A和點B的坐標,最后利用待定系數法可求得直線AB的解析式;
(2)E(m,0),則N(m,-![]() m+6),P(m,
m+6),P(m, ![]() +6),然后證明△ANE∽△ABO,依據相似三角形的性質可求得AN的長,接下來,再證明△NMP∽△NEA,然后依據相似三角形的性質可得到
+6),然后證明△ANE∽△ABO,依據相似三角形的性質可求得AN的長,接下來,再證明△NMP∽△NEA,然后依據相似三角形的性質可得到![]() ,從而可求得PM=12-
,從而可求得PM=12-![]() m,然后依據PM=
m,然后依據PM=![]() m+3m,然后列出關于m的方程求解即可;
m+3m,然后列出關于m的方程求解即可;
(3)①在(2)的條件下,m=4,則OE′=OE=4,然后再證明△OQE′∽△OE′A,依據相似三角形的性質可得到![]() ,從而可求得OQ的值,于是可得到點Q的坐標;
,從而可求得OQ的值,于是可得到點Q的坐標;
②由①可知,當Q為(2,0)時,△OQE′∽△OE′A,且相似比為![]() ,于是得到BE′+
,于是得到BE′+![]() AE′=BE′+QE′,當點B、Q、E′在一條直線上時,BE′+QE′最小,最小值為BQ的長.
AE′=BE′+QE′,當點B、Q、E′在一條直線上時,BE′+QE′最小,最小值為BQ的長.
本題解析:
(![]() )把點
)把點![]() 代入拋物線
代入拋物線![]()
得![]() ,
,
∴![]() ,
, ![]() ,
,
∴![]() 與
與![]() 軸交點,令
軸交點,令![]() ,
,
得![]() ,
,
∴![]() .
.
設![]() 為
為![]() 過
過![]() ,
, ![]() ,
,
∴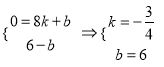 ,
,
∴![]() .
.
(![]() )∵過
)∵過![]() 作
作![]() 軸垂線交
軸垂線交![]() 于
于![]() ,交拋物線于
,交拋物線于![]() ,
,
∵![]() ,
,
∴![]() ,
, ![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,∴
,∴ ,
,
∴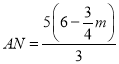 ,
,
∵![]() ,
,
∴![]() ,
,
又∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,∴
,∴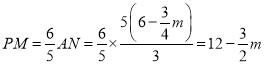 ,
,
∵![]() ,
,
∴![]()
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
, ![]() ,
,
∵![]() ,
,
∴![]() .
.
(![]() )①在(
)①在(![]() )的條件下,
)的條件下, ![]() ,∴
,∴![]() ,
,
設![]() ,∵旋轉,∴
,∵旋轉,∴![]() ,
,
若![]() ,
,
則![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,∴
,∴![]() ,
,
∴![]() .
.
②由①可知,當![]() 為
為![]() 時,
時,
![]() ,且相似比為
,且相似比為![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴當![]() 旋轉到
旋轉到![]() 所在直線上時,
所在直線上時, ![]() 最小,即為
最小,即為![]() 長度,
長度,
∵![]() ,
, ![]() ,
,
∴![]() ,
,
∴![]() 的最小值為
的最小值為![]() .
.


 舉一反三同步巧講精練系列答案
舉一反三同步巧講精練系列答案 口算與應用題卡系列答案
口算與應用題卡系列答案 名師點睛字詞句段篇系列答案
名師點睛字詞句段篇系列答案科目:初中數學 來源: 題型:
【題目】 如圖,在平面直角坐標系中直線y=x﹣2與y軸相交于點A,與反比例函數在第一象限內的圖象相交于點B(m,2).
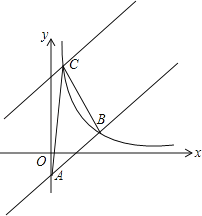
(1)求反比例函數的關系式;
(2)將直線y=x﹣2向上平移后與反比例函數圖象在第一象限內交于點C,且△ABC的面積為18,求平移后的直線的函數關系式.
查看答案和解析>>
科目:初中數學 來源: 題型:
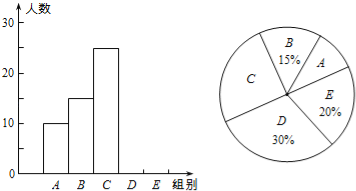
【題目】某校舉行“漢字聽寫”比賽,每位學生聽寫漢字39個,比賽結束后隨機抽查部分學生的聽寫結果,以下是根據抽查結果繪制的統計圖的一部分.
組別 | 正確字數x | 人數 |
A | 0≤x<8 | 10 |
B | 8≤x<16 | 15 |
C | 16≤x<24 | 25 |
D | 24≤x<32 | m |
E | 32≤x<40 | n |
根據以上信息解決下列問題:
(1)在統計表中,m= ,n= ,并補全條形統計圖.
(2)扇形統計圖中“C組”所對應的圓心角的度數是 .
(3)若該校共有900名學生,如果聽寫正確的個數少于24個定為不合格,請你估計這所學校本次比賽聽寫不合格的學生人數.
查看答案和解析>>
科目:初中數學 來源: 題型:
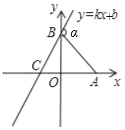
【題目】如圖,已知A點坐標為(5,0),直線y=kx+b(b>0)與y軸交于點B,∠BCA=60°,連接AB,∠α=105°,則直線y=kx+b的表達式為( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為了增強環境保護意識,在環保局工作人員指導下,若干名“環保小衛士” 組成了“控制噪聲污染”課題學習研究小組.在“世界環境日”當天,該小組抽樣 調查了全市 40 個噪聲測量點在某時刻的噪聲聲級(單位:dB),將調查的數據進行
處理(設所測數據均為正整數),得頻數分布表如下:
組別 | 噪聲聲級分組 | 頻數 | 頻率 |
1 | 44.5~59.5 | 4 | 0.1 |
2 | 59.5~74.5 | a | 0.2 |
3 | 74.5~89.5 | 10 | 0.25 |
4 | 89.5~104.5 | b | c |
5 | 104.5~119.5 | 6 | 0.15 |
合計 | 40 | 1.00 |
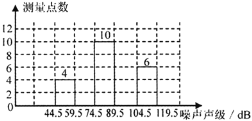
根據表中提供的信息解答下列問題:
(1)頻數分布表中的a= , b= , c= ;
(2)補充完整頻數分布直方圖;
(3)如果全市共有 300 個測量點,那么在這一時刻噪聲聲級小于 75dB 的測量點約有多少個?
查看答案和解析>>
科目:初中數學 來源: 題型:
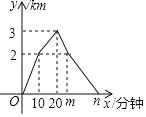
【題目】小明和爸爸周末到濕地公園進行鍛煉,兩人同時從家出發,勻速騎共享單車到達公園入口,然后一同勻速步行到達驛站,到達驛站后小明的爸爸立即又騎共享單車按照來時騎行速度原路返回,在公園入口處改為步行,并按來時步行速度原路回家,小明到達驛站后逗留了10分鐘之后騎車回家,爸爸在鍛煉過程中離出發地的路程與出發的時間的函數關系如圖.
(1)圖中m=_____,n=_____;(直接寫出結果)
(2)小明若要在爸爸到家之前趕上,問小明回家騎行速度至少是多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知△ABC是邊長為3的等邊三角形,點D是邊BC上的一點,且BD=1,以AD為邊作等邊△ADE,過點E作EF∥BC,交AC于點F,連接BF,則下列結論中①△ABD≌△BCF;②四邊形BDEF是平行四邊形;③S四邊形BDEF=![]() ;④S△AEF=
;④S△AEF=![]() .其中正確的有( )
.其中正確的有( )

A. 1個B. 2個C. 3個D. 4個
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com